강의 영상 출처 : https://www.youtube.com/watch?v=hE7eGew4eeg 

---

Few-shot Learning이란? 

매우 적은 수의 샘플을 기반으로 분류 또는 회귀를 수행하는 것을 의미한다.

 

위의 그림을 보면 Armadillo 사진 두 장, Pangolin(천산갑) 사진 두 장이 있다. 왼쪽의 4장의 사진을 보고 우리는 오른쪽의 사진이 천산갑이라는 사실을 잘 알아낼 수 있을 것이다. 즉, 4장의 사진만을 갖고도 카테고리를 잘 분류해낼 수 있다는 것이다.

 

그러나 컴퓨터도 그러할까? 컴퓨터가 위 둘을 구분하기에 4장의 사진은 너무 적을 것이다.

 

다음의 용어를 기억하자. : Support set & Query

 

Support set : A small set of samples. 모델을 학습시키기엔 굉장히 적은 수의 샘플들.

 

---

 

Few-shot learning은 supervised learning과는 다르다.

few-shot learning의 목표는 모델이 training set의 이미지를 인지하고 test set을 일반화하는 것이 아니다.

few-shot learning의 목표는 'Learn to Learn'이다.

 

'Learn to Learn'은 다음과 같이 이해하면 된다.

• 굉장히 큰 training set을 지닌 모델을 훈련시킨다.
• 훈련의 목표는 무엇이 코끼리인지, 무엇이 호랑이인지를 아는 것이 아니다.
• 목표는 안 보이는 코끼리와 호랑이들을 인지할 수 있는 것이 아니다.
• few shot learning의 목표는 객체 간의 유사점과 차이점을 아는 것이다.

 

훈련이 끝난 후, 당신은 두 개의 이미지를 모델에게 보여주며 두 동물이 같은 종류의 동물인지 물어볼 수 있을 것이다.

모델은 객체 간 유사점과 차이점을 알아냈을 것이고, 모델은 두 이미지가 같은 객체라는 것을 알려줄 수 있을 것이다.

 

training set를 확인해보자. training data는 5개의 클래스가 있고, 다람쥐 클래스가 포함되어 있지 않다.

그러므로 모델은 다람쥐를 인지하지 못할 것이다.

만약 모델에게 위에 다람쥐 사진 두 개를 보여주면 모델은 그것들이 다람쥐인지 모를 것이다.

그러나 둘이 비슷하다는 것을 알 수 있을 것이다.

그에 따라 모델은 위의 두 사진이 같은 종류인 것을 높은 확신을 갖고 알려줄 것이다.

그렇다면 위의 사진은 어떨까? 모델에는 천산갑과 멍멍이 클래스가 없다.

그러나 모델은 위 두 사진이 다르다는 것을 알 것이다.

그래서 위 두 사진은 다른 종류라는 것을 알려줄 수 있을 것이다.

질문을 달리 해보자. 모델에게 위의 Query를 주고 무엇인지 물어보면

위 객체는 training set에서 확인하지 못하는 클래스이기 때문에

모델은 답을 내주지 못할 것이다.

다음의 6개 추가적 정보를 모델에게 주어준다.

이제 모델은 query 이미지와 각각의 6개 support 이미지를 비교한 후 query 이미지가 otter 이미지와 가장 비슷한 것을 찾아낼 수 있을 것이다.

 

"Support set"은 meta learning의 특수 용어이다.

레이블링된 적은 수의 이미지 세트를 support set라고 칭한다.

 

training set = 모든 클래스의 샘플 수가 많다!

support set = 모든 클래스의 샘플 수가 적다!

 

support set로 학습을 할 수 있는 건 아니고 그저 test 때 추가적인 정보만을 부여하는 것이다.

 

위까지가 few-shot learning의 basic idea이다.

---

Few-shot learning & Meta Learning

 

Few-shot learning은 meta-learning의 일종이다.

meta-learning은 전통적 supervised learning과는 차이가 있다.

 

전통적 지도학습은 모델이 훈련 데이터를 인지했는지 묻고, 보지 못했던 테스트 데이터를 일반화한다.

그와는 다르게, meta learning의 목표는 learn to learn이다.

 

learn to learn을 어떻게 이해할 수 있을까?

 

당신이 아이를 데리고 동물원에 갔다고 가정하자.

아이는 처음으로 물에 사는 귀여운 수달을 마주했다.

그 후 다음의 동물 카드들을 주어줍니다.

아이는 동물원에 있는 동물이 수달이라는 사실을 가르침받은 적이 없으나,

카드의 수달과 마주하고 있는 동물이 동일하다는 사실을 알아낼 수 있을 것이다.

이는 아이에게 동물이 수달이라고 가르치는 것이 아닌,

아이가 스스로 배우도록 가르친 것이고 이러한 과정을 'meta-learning'이라고 한다.

 

다시 한 번 Supervised learning과 few shot learning의 차이에 대해 살펴보도록 하자.

 

우선 모델은 대규모 훈련 셋에 의해 학습된다.

 

Supervised learning의 경우

• 테스트 샘플들은 이전에 한 번도 보지 못했던 것들이다. (훈련 셋에 없는 데이터)
• 그러나 테스트 샘플들은 모델이 아는 클래스에 속해 있다.

 

Few-shot learning의 경우

• Query 샘플들은 이전에 한 번도 보지 못했던 것들이다.
• 그리고 Query 샘플들은 모델이 알지 못하는 클래스이다. <- 이것이 Supervised learning과의 가장 큰 차이이다.
• 그렇기 때문에 모델에게 추가적 정보를 더 제공해주어야 한다. (Support Set)
• query와 support set을 비교하며 모델은 가장 비슷한 클래스를 찾아낸다.

그렇게 train set에서 보지 못한 데이터에 대해서 추가적 정보를 주어주기 위해 Support Set이 필요한데,

여기에서 k-way n-shot Support Set의 개념이 나온다.

 

k-way란? Support set이 같는 k개의 클래스들을 의미한다.

n-shot이란? 모든 클래스들이 갖는 n개의 샘플 수를 의미한다.

 

즉, 위 사진 같은 경우는 6개의 클래스가 각각 1개의 샘플을 갖는

6-way 1-shot Support Set이 되는 것이다.

 

few-shot learning의 정확도같은 경우 way(Support Set의 클래스 수)가 많아지면 많아질수록 더 떨어진다.

이는 생각해보면 간단한 문제다.

객관식 문제를 푼다고 생각했을 때, 답안이 3개가 있는게 쉬운가, 6개가 있는게 쉬운가?

3개가 있는게 훨씬 답을 찾아내기 쉬울 것이다.

이와 같이 few-shot learning도 way가 많아지면 많아질수록 답을 찾아내기 버거워하는 것이다.

반대로 shot(Support Set 각 클래스 별 샘플 수)은 많아지면 많아질수록 정확도가 더 상승한다.

문제에 대한 예시가 많아질수록 더 답을 찾아내기 수월해질 것이기에 정확도가 상승할 수 밖에 없을 것이다.

---

Few-shot learning basic idea

 

few-shot learning의 기본 아이디어는

유사성을 예측하는 함수 -> sim(x, x')

를 훈련시키는 것이다.

위의 예제에서 각각의 similarity를 계산하면 다음과 같은 결과가 나올 것이다.

 

sim(x1, x2) = 1 -> x1과 x2는 유사한 object

sim(x1, x3) = 0 -> x1과 x3는 다른 object

sim(x2, x3) = 0 -> x2와 x3는 다른 object

 

위와 같은 아이디어는 다음과 같이 구현될 수 있다.

 

1. large-scale 훈련 데이터셋을 통해 유사성 함수를 훈련한다.
2. 유사성 함수를 prediction에 적용한다.
   1. support set에 있는 모든 샘플을 query와 비교한다.
   2. 가장 유사성 점수가 높은 샘플을 찾는다.

이제 이 few-shot learning을 구현하기 위한 네트워크 구조에 대해서 살펴보도록 하자.

---

Siamese Network (샴 네트워크)

 

Preparing Training Dataset

 

Siamese Network를 학습하기 위한

training set은 다음과 같이 positive samples과 negative samples로 구성된다.

 

CNN for Feature Extraction

 

train dataset이 구성되었다면, feature extraction을 위한 CNN 모델을 구성한다.

 

Training Siamese Network

 

이제 훈련 데이터를 이용해 모델을 학습 시킨다.

• f : cnn for feature extraction. 같은 신경망임.
• h1, h2 : feature vectors about x1 and x2
• z : |h1 - h2| 두 feature vector 사이의 차이. 

모델은 두 개의 파트로 이뤄져 있다.

하나는 CNN(f). input image의 feature를 extracting해준다.

input image가 두 개이기 때문에 두 개의 CNN이 적용되는데,

이 때 두 개의 CNN은 같은 CNN(같은 구조. 같은 모델 파라미터.)임을 명심하자.

다른 하나는 fully connected layers(Dense layers)로

vector z를 0에서 1사이의 스칼라 값으로 mapping해준다.

 

훈련 중에는 두 파트(f, z) 모두 업데이트된다.

 

역전파를 통해 gradient는 loss 함수에서 z vector와 dense layer의 parameter로 흐른다.

이 때 gradient를 통해 경사 하강법에 의해 매개변수가 업데이트된다.

 

더 나아가 gradient가 Convolutional layer에도 넘어가 마찬가지로 f의 매개변수 또한 업데이트된다.

---

One-Shot Prediction

 

학습을 마친 후 모델을 one-shot prediction에 활용할 수 있다.

다음 예제를 보자.

6-way 1-shot Supprot Set과 다람쥐 객체가 있는 이미지가 Query로 주어지고 있다.

우리는 모델을 통해 Query와 Supprot Set에 있는 한 이미지를 1:1로 비교할 수 있다.

비교 결과는 다음과 같이 나올 것이다.

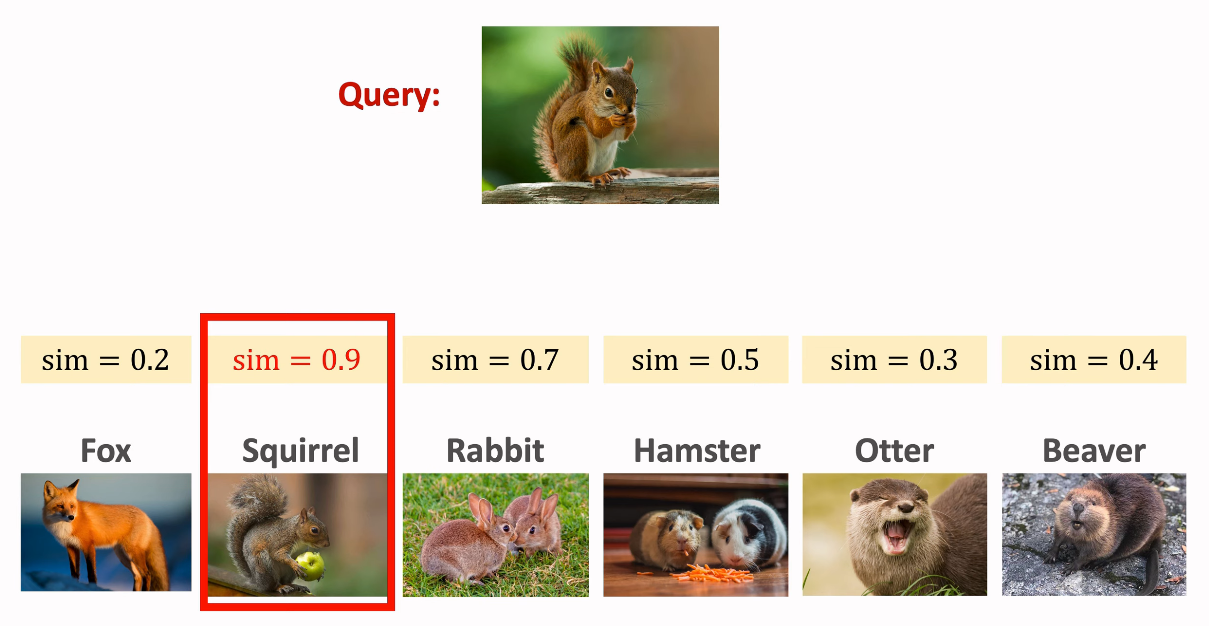
나온 결과 중 Support Set의 Squirrel(다람쥐) 클래스 이미지와 Query 이미지가 유사성이 가장 높기 때문에 우리는 Query가 다람쥐 클래스라는 결론을 도출해낼 수 있게 된다.

---

Triplet Loss

 

Preparing Training Dataset

 

아까와는 살짝 Training Dataset을 구성하는 방법이 달라진다.

1. 클래스에서 한 데이터를 랜덤하게 선택한다. 이를 anchor라고 칭한다.
2. 같은 클래스에서 다른 데이터를 랜덤하게 선택한 후, 이를 Positive Sample로 활용한다.
3. 이제 선택한 클래스가 아닌 그 외의 클래스를 랜덤하게 선택하고, 정해진 클래스 내에서 랜덤하게 데이터를 선택하여 이를 Negative Sample로 활용한다.

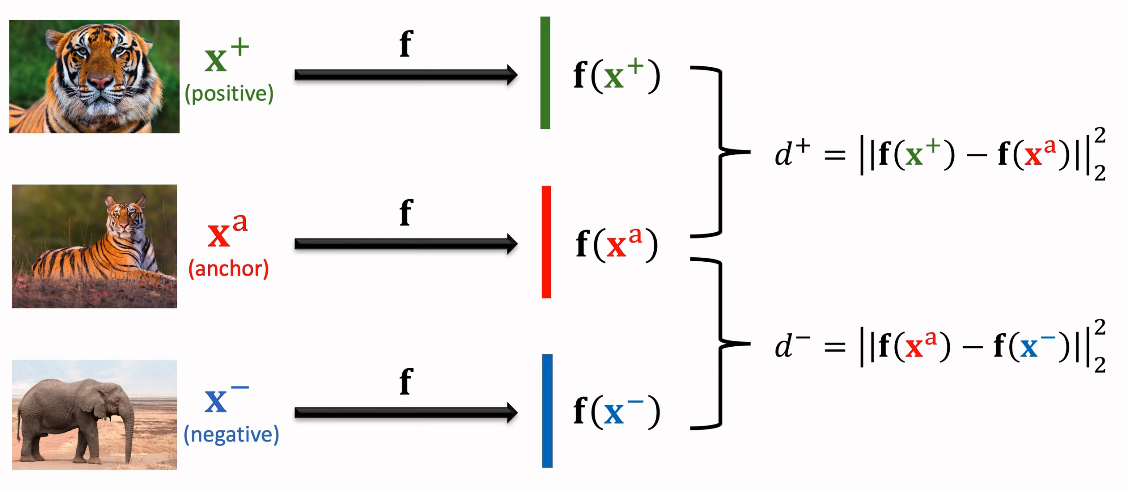
그러면 다음과 같이 세 개의 데이터가 선정되게 될 것이다.

이 세 개의 데이터에 같은 CNN f를 적용해주어 feature들을 extrating한다.

그 후에 postive sample feature와 anchor sample feature의 distance d+와

negative sample feature와 anchor sample feature의 distance d-를 구한다.

이렇게 구한 d+는 같은 클래스 사이의 거리이기 때문에 값이 작을 것이고,

d-는 다른 클래스 사이의 거리이기 때문에 값이 클 것이다.

이를 시각화하면 다음과 같이 나타날 것이다.

그러나 이러한 결과를 낸다고 해도 모델이 호랑이와 코끼리를 구분할 수는 없다.

 

위의 아이디어를 기반으로 loss function을 정의하자.

d+는 positive sample과 anchor sample 간 L2 제곱 거리이다. 

그리고 두 샘플은 같은 클래스기 때문에 거리가 가까워야 할 것이므로,

d+의 값이 작아지도록 해야 한다.

반대로 d-는 negative sample과 anchor sample 간 L2 제곱 거리로,

거리가 멀어야 하므로,

d-의 값이 크도록 해야 할 것이다.

 

우리는 α라는 margin을 정의할 것이다.

α는 양수이며 tuning hyper parameter이다.

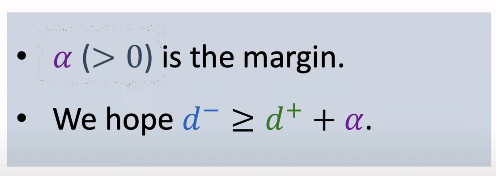
만약 d+와 α를 더한 값이 d-보다 작다면 classification이 제대로 수행된 것으로 판단하여, loss 값은 0이 된다.

그러나 그 반대의 경우라면 loss의 값을 d+ + α - d-로 설정하여 loss가 작아지도록 한다.

loss가 작다는 것은 d+가 작다 즉, positive와 anchor 사이의 feature space가 가까워지는 것을 의미하게 되며,

negative와 anchor 사이에서는 feature sapce가 멀어지며 확실하게 분리될 수 있도록 한다.

 

그래서 최종적으로 아래와 같은 loss function(max{0, d+ + α - d-})을 얻게 된다.

이와 같은 loss를 triplet loss라고 한다.

이는 anchor sample, postivie sample, negative sample로 이뤄진 세 쌍둥이 샘플을 기반으로 구해지는 loss라서 triplet loss라고 칭한 듯하다.

 

이제 아까와 똑같은 예시를 갖고 위의 과정을 통해 훈련된 Siamese Network가 어떤 식으로 결과를 도출할지 알아보자.

주어진 Support Set과 Query는 아까 확인한 예제와 같다. (6 shot 1 way Support Set & Squirrel Query)

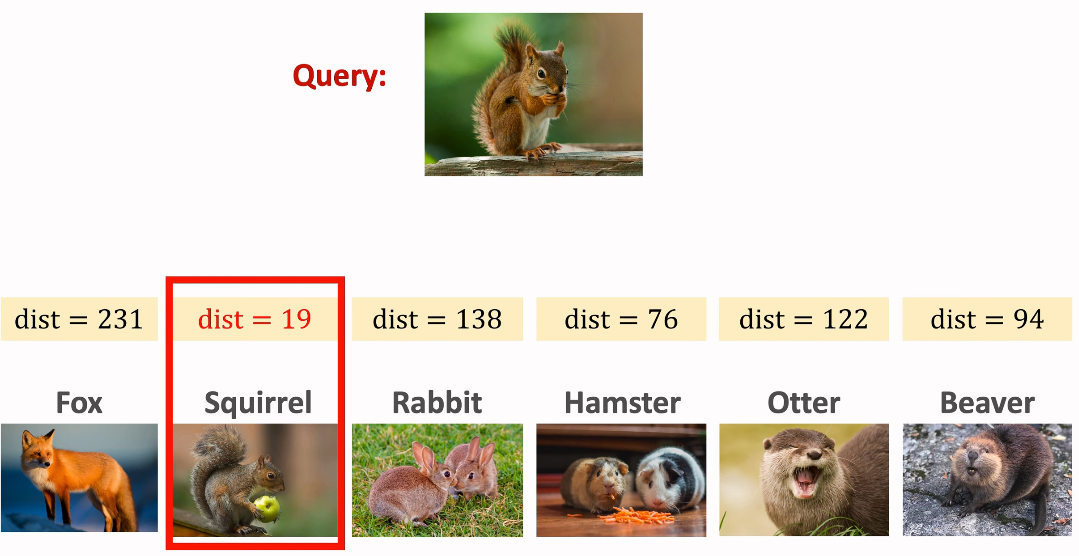
위와 같이 Query 이미지와 Support Set 각 이미지에 대한 distance가 결과로 나오게 되는데

이를 통해  Query 이미지와 Squirrel Support Set이 가장 짧은 거리를 가진 것을 확인할 수 있고,

Query 이미지가 Squirrel 클래스라는 것을 알 수 있게 된다.

---

Pretraining and Fine tuning

 

preliminary

 

Cosine Similarity

 

두 벡터간 similarity 계산.

 

ex)

x와 w 벡터가 있다.

이 두 벡터는 unit vector(길이가 1인 벡터)라고 가정한다.

||x||_2 = 1 & ||w||_2 = 1

 

이는 두 벡터의 L2 norm이 1로 같다는 것을 의미한다.

 

이 때 x와 w 벡터는 unit vector이기 때문에

cosine Θ는 x와 w의 inner product(내적)와 같다.

cosine Θ는 x와 w 사이의 유사성을 계산할 수 있다.

 

cosine similarity는 다음과 같은 식으로 이해할 수 있다.

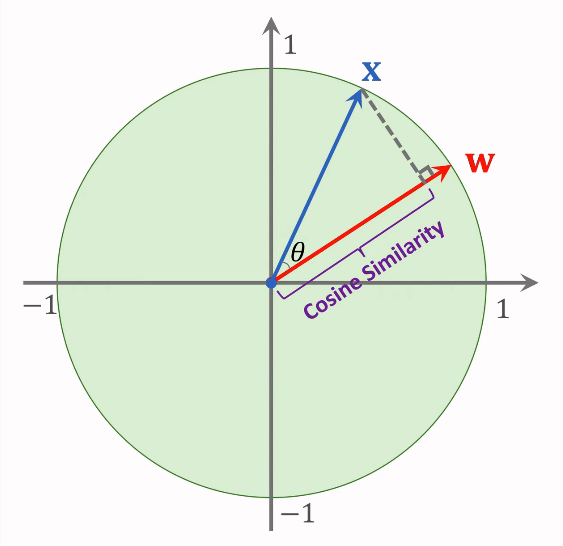
벡터 x를 w에 걸쳐 있는 선에 투영한다.(회색 점선)
투영의 길이가 바로 코사인 유사도가 된다.

 

만약 x와 w가 unit vector가 아니라면 cosine similarity를 계산하기 전

두 벡터를 unit vector로 normalize해 줄 수 있을 것이다.

cosine similarity는 다음의 방정식으로 도출해낼 수 있다.

x 벡터와 w 벡터 각각 normalize한 후

그들의 inner product(=cosine similarity)를 계산한다.

---

Softmax Function

 

굉장히 흔하게 사용되는 activation 함수이다.

이는 벡터를 확률 분포로 mapping한다.

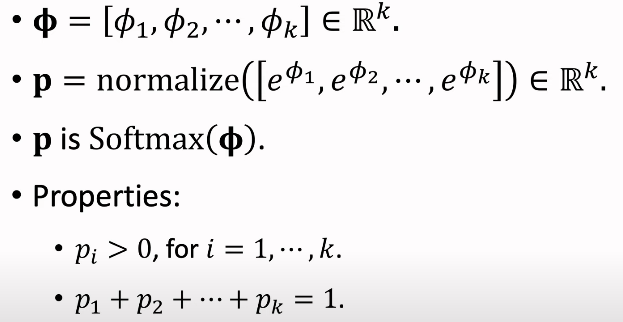
input은 Φ(phi)이며 k차원 벡터이다.

softmax는 k postive numbers를 얻기 위해서 모든 Φ의 k개 elements들에 exponential function을 적용하고

normalize한다. 

 

이 때 input과 output은 모두 k차원 벡터이며

output vector p의 모든 요소는 모두 양수이고, 다 합치면 1이 되어

p는 확률 분포가 되게 된다.

 

softmax는 multi-class classifier output에 적용된다.

위는 softmax의 예시이다.

softmax 함수는 값이 가장 큰 항목은 더 크게 만들고, 다른 항목은 작게 만든다.

왜 이를 softmax라고 부를까?

만약 우리가 max 함수를 사용하면 가장 큰 항목은 1로 mapping되고 나머지는 0으로 mapping된다.
그러나 softmax는 max 함수와 역할은 유사하나 극단적으로 큰 항목을 1로 변환하지는 않고

작은 항목을 0으로 변환하지는 않는다. 과하지 않게 max를 적용한다고 생각하면 될 듯.

 

Softmax Classifier

 

Softmax classifier은 dense layer와 softmax activation으로 구성된다.

classifier의 input은 feature vector x이다.

x에 parameter matrix w를 적용하고, vector b를 더한다.

마지막으로 softmax function을 적용한다.

그러면 vector p가 output으로 나오게 된다.

만약 클래스 개수가 k개라고 하면, vector p는 k차원일 것이다.

 

위에서 matrix w와 vector b는 softmax classifier에서 trainable한 파라미터이다.

matrix w는 k개의 행을 갖는다. k는 클래스의 개수이며, 모든 행은 클래스에 해당한다.

---

Few-Shot Prediction Using Pretrained CNN

 

Pretraining

 

이전에 앞서 보았던 것처럼 feature extration을 위한 CNN을 준비한다. (aka embedding)

위 CNN은 표준 지도 학습이나 샴 네트워크를 통해 pretrained 될 수 있다.

 

feature prediction method

위 예제는 3-way 2-Shot Support Set을 나타낸다.

각 이미지에 CNN을 적용해 feature vector를 얻어낸다.

위 예제는 클래스 당 2개의 샘플이 있으므로 각 두 개의 feature vector가 나올 것이다.

이 때 나온 두 feature vector의 제곱 평균을 내어 평균 vector를 구한다.

 

위 예제는 세 개의 클래스가 있으므로 세 개의 mean vector가 나올 것이다.

그 후 세 개의 mean vector를 normalize해주어 unit vector로 변환하여준다.

각 unit vector는 μ1, μ2, μ3으로 나타낸다.

μ 벡터는 future prediction 때 euclidean 공간에서 각 클래스의 embedding이다.

이를 query와 비교할 것이다.

 

Making Few-shot Prediction

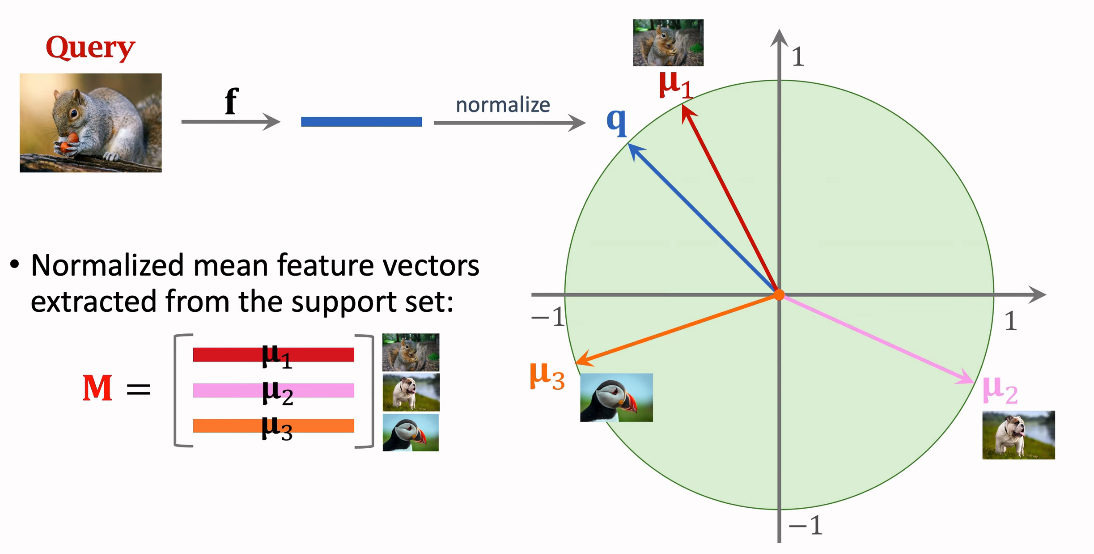
query 이미지에 CNN을 적용해 feature를 extracting하고, 이를 normalize해서

unit vector로 변환한다. 이를 q라고 하자.

그리고 우리는 앞서 Support set에서 세 개의 μ 벡터를 구했다.

이 세 개의 μ 벡터를 쌓은 matrix를 M이라고 하자.

각 μ 벡터는 matrix M의 행이 된다.

 

이제 prediction을 만들어보자.

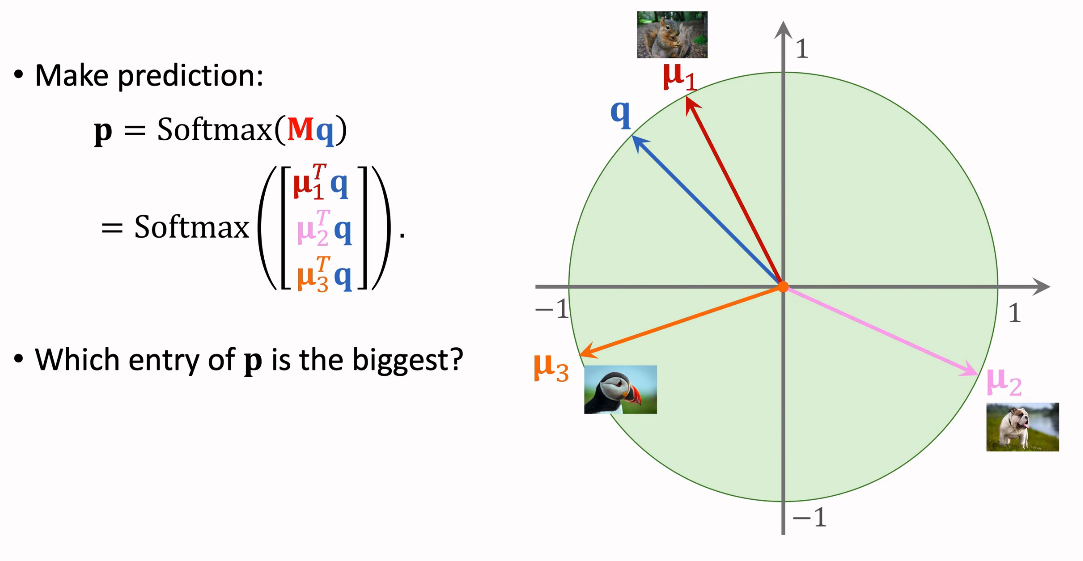
matrix M과 q에 Softmax를 적용하자. 

세 항목 중 가장 값이 큰 것은 명백히 첫 번째 항목일 것이다.

그렇기 때문에 모델은 query 이미지가 첫 번째 이미지인 squirrel이라고 예측해낼 수 있을 것이다.

---

Fine-Tuning

 

앞서 우리는 pre-trained model을 통해 예측을 진행하였다.

이제 여기에 더하여 pre-training 이후에 fine tuning을 수행할 수 있다.

최근 연구는 fine-tuning이 예측 정확도를 높일 수 있다는 사실을 입증했다.

 

Few-Shot Prediction Using Pretrained CNN

 

(x_j, y_j)로 이뤄진 support set의 sample이 있다고 가정하자.

여기서 x_j는 이미지이고,

y_j는 레이블이다.

 

f(x_j)는 pretrained CNN에 의해 추출된 특징 벡터이다.

 

p_j = Softmax(W ● f(x_j) + b)는 확률 분포이다.

이 때 W는 세 개의 클래스를 지닌 Support set이라 가정한다.

그러면 p_j는 세 개의 클래스에 대한 확률 혹은 confidence score가 된다.

 

이전에 우리는 fine tuning을 이용하지 않고, W와 b를 데이터로부터 학습하는 것대신

단순히 W=M으로, b=0으로 고정했다.

 

이에 대한 Fine tuning으로 Support Set을 통해 W와 b를 학습되도록 한다.

W와 b는 다음과 같은 방법으로 학습될 수 있다.

• CrossEntropy를 활용해서 y_j와 예측값인 p_j의 차이를 계산한다. -> loss
• 나온 CrossEntropy들을 합한 값을 목적 함수로 사용한다. (support set의 모든 샘플들의 loss를 더한 값)
• minimization은 p_j가 ground truth y_j로 접근하도록 한다.
  
  • Optimization variable
    • W and b
    • Parameters of the CNN
• 과적합을 방지하기 위해 Regularization을 사용한다.
  • 최근 연구에서는 entropy regularization을 추천한다.

 

Benefit of fine tuning

• fine tuining은 예측 정확도를 상당히 향상시켰다.
  • 5-way 1-shot에서 2%~7% 정확도 향상
  • 5-way 5-shot에서 1.5%~4% 정확도 향상
• 그 외 다른 연구에서도 비슷한 결론이 나옴.
• 정교한 SOTA methods들과 비교할만 함.

---

 Fine-Tuning Trick 1 : A Good Initialization

 

예측값은 sofmax classifier에 의해 나온다.

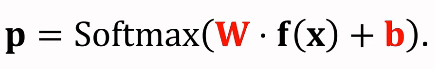
이 때 W와 b는 학습 가능한 파라미터로, 이 두 파라미터를 잘 초기화하는 것은 굉장히 도움이 된다.

특히 support set의 크기가 작을 때 랜덤하게 초기화하는 것은 좋은 조건이 아니다.

 

랜덤하게 초기화하는 대신 W=M으로, b=0으로 초기화하는 것이 좋다.

 

Fine-Tuning Trick 2 : Entropy Regularization

 

Softmax classifier는 작은 supprot set에 의해 학습되기 때문에 과적합이 발생할 수 있다.

이 때 과적합 방지를 위해 entropy regularization을 추천하고 있다.

 

x는 query 샘플이다.

 

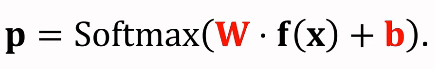
f(x)는 이미지에서 추출된 특징 벡터로, softmax classifier의 input값이다.

p는 softmax classifier에 의해 나온 예측값이며 확률 분포이다.

 

entropy를 통해 퍼져 있는 분포를 계산할 수 있다.

p_i는 벡터의 i번째 요소이다.

p의 모든 요소에 대해 p_i * log(p_i)를 계산 후 음수로 만든다.

 

이렇게 하면 모든 쿼리에 대해 entropy가 나오게 된다.

그리고 이에 대한 평균을 구하는 것이 entropy regularization이다.

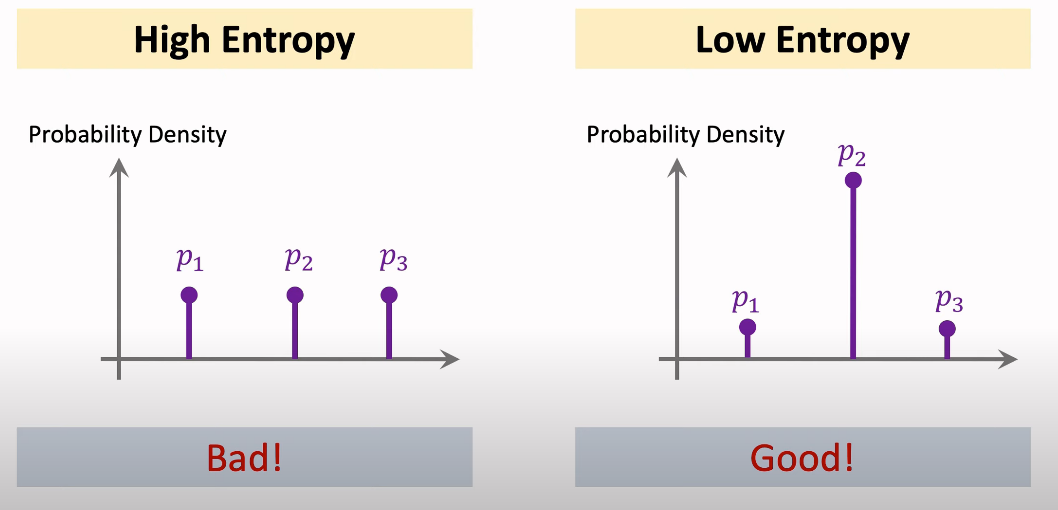
entropy가 높을수록 classifier가 제대로 일을 하지 못하고 있다는 의미이므로,

entropy를 최대한 작게 만들어주어야 한다.

 

Fine-Tuning Trick 3 : Cosine Similarity + Softmax Classifier

 

앞서 봤던 Softmax Classifier에서 inner product를 cosine similarity로 교체하는 방법이다.

여기서 Consine similarity는 normalization 이후 내적값이다.

w와 q를 l2 norm으로 나누어 normalize한 값이다.

우선 궁극적인 이유를 살펴보기 전에 Loss란 무엇인지에 대해서 알아보자.

 

기본적 수준에서 Loss function은 데이터 세트의 입력 데이터 포인트를 분류할 때 주어진 예측이 얼마나 좋은지 나쁜지를 수량화한다.

 

Loss가 작을수록 classifier은 입력 데이터와 출력 대상 간 관계를 모델링하는 데 더 나은 작업을 수행한다.

 

Loss function에는 다음과 같은 것들이 있다.

 

• Binary cross entropy
• Categorical cross entropy
• Sparse categrical cross entropy
• Mean Squared Error (MSE)
• Mean Absolute Error (MAE)
• Standard Hinge
• Squared Hinge

Loss에 대해서는 다음과 같은 정도를 알아두도록 하자.

• Loss는 모델이 얼마나 좋은지에 대한 정도를 측정하는 것이다.
• loss가 작을수록 더 좋다.
• 그러나 과적합에 대해 조심할 필요가 있다.

---

이제 왜 검증 데이터에서의 loss가 훈련 데이터에서의 loss보다 낮은지에 대한 이유를 알아보자.

 

첫 번째 이유 : 훈련 중에는 Regularization이 적용되었으나, 검증 / 테스트 중에는 적용되지 않았다.

 

우리는 모델을 학습시킬 때 정규화를 활용한다. 정규화를 활용하면 다음과 같은 효과를 얻을 수 있다.

• 더 높은 검증 / 테스트 정확도를 확보할 수 있다.
• 검증 및 테스트 세트 외부 데이터로 더 잘 일반화할 수 있다.

정규화 방법은 종종 검증 / 테스트 정확도 개선을 위해 훈련 정확도를 희생한다. 어떤 경우엔 검증 손실이 훈련 손실보다 낮아질 수 있다.

그리고, dropout과 같은 정규화 방법은 검증 / 테스트 시 적용되지 않는다는 점에 유의하라.

---

두 번째 이유 : 각 Epoch 동안 Training Loss를 측정하고, 각 Epoch 후에 Validation Loss를 측정한다.

 

훈련 손실은 전체 epoch동안 지속적으로 보고되나, 검증 metric은 현재 훈련 에포크가 완료된 후에만 검증 세트에 대해 계산된다.

---

세 번째 이유 : 검증 세트가 훈련 세트보다 쉬울 수 있거나 누출이 있을 수 있다.

 

• 검증 세트가 훈련 세트와 동일한 분포에서 샘플링 되었음을 보장할 수 있는가?
• 검증 예제가 훈련 이미지만큼 어렵다 확신하는가?
• 훈련 샘플이 실수로 검증 / 테스트 샘플과 혼합되지 않았다 확신할 수 있는가?
• 코드가 훈련, 검증 및 테스트 분할을 올바르게 생성했다 확신하는가?

---

보너스 : 당신은 진짜 열심히 훈련하고 있는가?

 

우리는 과적합을 방지하기 위해 다음과 같은 테크닉을 사용하곤 한다.

• Dropout
• L2 weight decay
• 모델 용량 감소 (더 얕은 모델로 작성)

모두 훌륭하고 좋으나 때때로 모델을 과도하게 정규화하게 된다.

위의 세 가지 테크닉을 모두 사용하고 있다면 모델이 과도하게 정규화됐을수 있다. 

다음을 통해 정규화 제약을 완화해보도록 하자.

• L2 weight decay 강도를 줄인다.
• Dropout 양을 줄인다.
• 모델 용량을 늘린다. (모델을 더 깊게 만든다.)

위와 같이 완화시키게 된다면 더 큰 학습률로 훈련을 시도하는 등의 파라미터 변화가 필요할 것이다.

---

참고

 

https://pyimagesearch.com/2019/10/14/why-is-my-validation-loss-lower-than-my-training-loss/

C++ 이론 기초

---

C++ 언어 설계 목표 4가지

 

1. C언어로 작성된 프로그램과의 호환성
2. 객체 지향 개념 도입으로 소프트웨어 재사용 가능
3. 엄격한 타입 체크. 실행 시간 오류 가능성 ↓, 디버깅을 도움.
4. 실행 시간 효율성 저하 최소화

 

C 언어에서 더 추가된 기능

 

• 함수 중복(fucntion overloading) - 매개 변수 개수나 타입이 서로 다른 동일한 이름 함수들을 선언할 수 있게 함
• 디폴트 매개 변수(default parameter) - 매개 변수에 값이 전달되지 않은 경우 디폴트 값이 전달되도록 함수 선언 가능
• 참조(reference)와 참조 변수 - 변수에 별명을 붙여 변수 공간을 같이 사용할 수 있는 참조 개념 도입
• 참조에 의한 호출(call-by-reference) - 함수 호출 시 참조를 전달할 수 있게 함
• new와 delete 연산자 - 동적 메모리 할당, 해제를 위한 연산자
• 연산자 재정의(operator overloading) - 기존 연산자에 새로운 연산을 정의할 수 있게 함
• 제네릭 함수와 클래스(generics) - 함수나 클래스를 데이터 타입에 의존하지 않고 일반화시킬 수 있게 함.

 

C++ 객체 지향 특성

 

• 객체와 캡슐화(Encapsulation)
  
  • 캡슐화란? 데이터를 캡슐로 싸 외부 접근으로부터 데이터를 보호하는 객체 지향 특성.
    C++에서의 캡슐 - 클래스
    클래스는 객체를 정의하는 틀이며, 객체는 클래스를 통해 생겨난 실체(instance)
    클래스는 멤버 변수들과 멤버 함수들로 이뤄짐. public / private으로 공개할 지 안 할지 결정 가능.
    프로그램 개발 시, 멤버 변수들은 private, 일부 멤버 함수들은 public으로 하여 간접적으로 멤버 변수에 접근하게끔 하는 방식이 좋다.
  • 예시
    

    class Circle {
      private:
        int radius;
      public:
        Circle(int r) { radius = r; }
        double getArea() { return 3.14*radius*radius; }
    };​

• 상속성(Inheritance)
  • 상속이란? 자식 클래스의 객체가 생성될 때 자식 클래스에 선언된 멤버뿐 아니라 부모 클래스에 선언된 멤버들도 함께 가지게 되는 특성. 코드의 재사용성을 높여준다.
  • 예시
    

    class Figure {
      void getLength();
      void getArea();
    };​

    class Circle : public Figure {
      void painting(); 
    };​

    Circle이 Figure 클래스로부터 상속을 받아 getLength()와 getArea() 기능을 사용 가능하게 된다.
• 다형성(Polymorphism)
  
  • 다형성이란? 하나의 기능이 경우에 따라 서로 다르게 보이거나 다르게 작동하는 현상.
  • 예시
    (+) 연산자
    - 정수 덧셈 ( 3 + 5 -> 8 )
    - 문자열 연결 ( "Friend" + "ship" -> "Friendship" )
    - Square 객체 + Square 객체 -> Rectangle 객체
    - void getInfo(int age) { ... }
      void getInfo(int age, string name) { ... }
      void getInfo(int age, string name, string phone) { ... }
    위와 같은 예시들을 연산자 중복(operator overloading)이라고 부른다. 
    함수와 같은 경우는 함수 중복(function overloading)이라고 한다. 모든 함수가 각각 서로 다른 함수로 다뤄진다.
  • 다형성은 상속 관계에서도 나타난다. 이는 부모 클래스에 구현된 함수를 동일한 이름으로 자식 클래스에서 다르게 구현하는 함수 재정의 혹은 함수 오버라이딩(function overriding)으로 불린다.

 

C++ 언어와 제네릭 프로그래밍

 

제네릭 프로그래밍(generic programming) : 동일한 프로그램 코드에 다양한 데이터 타입을 적용할 수 있도록 함수와 클래스를 일반화시킨 제네릭 함수(generic function)와 제네릭 클래스(generic class)를 만들고, 개발자가 원하는 데이터 타입을 적용시켜 프로그램 코드를 틀에서 찍어내듯 생산하는 기법이다.

 

C++ 프로그램 개발 과정

 

1. C++ 소스 프로그램 작성(source program)
2. 컴파일(compile) : C++ 소스 프로그램이 문법에 맞게 작성되었는지 검사 후, 기계어 코드로 변환해 목적 파일(object file)을 생성하는 과정.
3. 링킹(linking) : 어떤 목적 파일이 참조하는 C++ 표준 라이브러리나 다른 목적 파일 속에 있는 함수, 객체, 데이터를 포함해 실행에 필요한 모든 기계어 코드를 확보해 하나의 실행 파일로 만드는 과정.
   ※ DLL - 실행 중 필요한 순간에 결합하도록 만들어진 라이브러리. 실행 파일 크기를 줄이며, 여러 응용프로그램이 실행 중에 공유한다.
4. 하나의 실행 파일(executable file) 완성!

 

C++ 표준 라이브러리

 

C++ 표준 라이브러리는 개발자들이 불러 쓸 수 있는 다양한 종류의 함수와 클래스가 컴파일된 목적 파일들. 다음의 세 그룹과 기타 기능으로 나뉜다.

• C 라이브러리 : 기존 C 표준 라이브러리를 수용해 C++에서 사용할 수 있게 한 함수들. 이름이 c로 시작하는 헤더 파일에 선언됨.
• C++ 입출력 라이브러리 : 콘솔 및 파일 입출력을 위한 함수와 클래스들로서, 제네릭 프로그래밍을 지원하기 위해 템플릿으로 작성. 
• C++ STL 라이브러리 : 제네릭 프로그래밍을 지원하기 위해 템플릿으로 작성된 유용한 함수와 클래스를 포함하는 라이브러리.

• C 라이브러리	C++ 입출력 라이브러리	C++ STL 라이브러리
  - csetjmp - cassert - csignal - cctype - cstdarg - cerrno - cstddef - cfloat - cstdio - ciso646 - cstdlib - climits - cstring - clocale - ctime - cmath	- fstream - strstream - iomanip - streambuf - ios - iosfwd - iostream - ostream - istream - sstream	- exception - list - stack - locale - stdexcept - functional - map - memory - string - numeric - typeinfo - utility - queue - valarray - iterator - set - vector - deque - limits - new ※ <new> 헤더 파일은 STL에 포함되지 않는 기타 기능을 구현했음.

 

 

 

Real-time Streams

Real-time timestmaps

Mediapipe calculator 그래프는 interactive 어플리케이션을 위한 비디오 또는 오디오 프레임의 스트림을 처리하는 데 자주 사용됩니다. Mediapipe 프레임워크는 연속적 패킷에 단조롭게 증가하는 타임스탬프를 할당하기만 하면 됩니다. 관례에 따라 실시간 Calculator와 그래프는 기록 시간 또는 각 프레임의 표시 시간을 타임스탬프로 사용하며, 각 타임스탬프는 1월 1일 이후 마이크로초를 나타냅니다.

---

Real-time shceduling

일반적으로 각 Calculator는 주어진 타임스탬프에 대한 모든 입력 패킷을 사용할 수 있게 되는 즉시 실행됩니다. 일반적으로 이것은 Calculator가 이전 프레임 처리를 완료하고 입력을 생성하는 각 Calculator가 현재 프레임 처리를 완료했을 때 발생합니다. Mediapipe 스케쥴러는 이러한 조건이 충족되는 즉시 각 Calculator를 호출합니다.

---

Timestamp bounds

Calculator가 주어진 타임스탬프에 대해 출력 패킷을 생성하지 않으면 대신 해당 타임스탬프에 대해 패킷이 새성되지 않음을 나타내는 Timestamp bounds를 출력할 수 있습니다. 이 표시는 해당 타임스탬프의 특정 스트림에 대해 패킷이 도착하지 않은 경우에도 다운스트림 Calculator가 해당 타임스탬프에서 실행되도록 하는데 필요합니다. 이는 각 계산기가 가능한 한 빨리 처리를 시작하는 것이 중요한 interactive 어플리케이션의 실시간 그래프에 특히 중요합니다.

그래프가 다음을 따름을 생각하십시오.

node {
  calculator : "A"
  input_stream : "alpha_in"
  output_stream : "alpha"
}
node {
  calculator : "B"
  input_stream : "alpha"
  input_stream : "foo"
  output_stream : "beta"
}

가정 : 타임스탬프 T에서 노드 A는 출력 스틀미 알파로 패킷을 보내지 않습니다. 노드 B는 타임스탬프 T에서 foo 패킷을 받고 타임스탬프 T에서 알파 패킷을 기다리고 있습니다. A가 B에게 알파에 대한 타임스탬프 바운드 업데이트를 보내지 않으면 B는 패킷이 알파로 도착할 때까지 계속 기다립니다. 한편, foo 패킷 큐는 T, T+1 등에서 패킷을 누적합니다.

스트림에서 패킷을 출력하기 위해 Calcualtor는 API 함수 CalculatorContext::Outputs 및 OutputStream::Add를 사용합니다. 대신 스트림에 바인딩된 타임스탬프를 출력하기 위해 Calculator는 API 함수 CalculatorContext::Outputs 및 CalcualtorContext::SetNextTimestmapBound를 사용할 수 있습니다. 지정된 경계는 지정된 출력 스트림 다음 패킷에 대해 허용되는 가장 낮은 타임스탬프입니다. 패킷이 출력되지 않으면 Calcualtor는 일반적으로 다음과 같은 작업을 수행합니다.

cc->Outputs().Tag("output_frame").SetNextTimestampBound(
  cc->InputTimestamp().NextAllowedInStream());

Timestamp::NextAllowedInStream 함수는 연속적인 타임스탬프를 반환합니다. ex) Timestamp(1).NextAllowedInStream() == Timestamp(2)

---

Propagating timestamp bound

실시간 그래프에 사용되는 Calculator는 다운스트림 Calculator를 즉시 예약할 수 있도록 입력 타임스탬프 경계를 기반으로 출력 타임스탬프 경게를 정의해야 합니다. 일반적 패턴은 Calculator가 입력 패킷과 동일한 타임스탬프를 가진 패킷을 출력하는 것입니다. 이 경우 Calcualtor::Process를 호출할 때마다 패킷을 출력하는 것만으로도 출력 타임스탬프 경계를 정의하기에 충분합니다.

그러나 Calculator는 출력 타임스탬프에 대해 이 일반적 패턴을 따를 필요가 없으며 단조롭게 증가하는 출력 타임스탬프를 선택하기만 하면 됩니다. 결과적으로 특정 Calculator는 타임스탬프 경계를 명시적으로 계산해야 합니다. MediaPipe는 각 계산기에 대한 적절한 타임스탬프 경계를 계산하기 위한 여러 도구를 제공합니다.

1. SetNextTimestampBound() 는 출력 스트림에 대해 타임스탬프 경계 t+1을 지정하는 데 사용할 수 있습니다.

cc->Outputs.Tag("OUT").SetNextTimestampBound(t.NextAllowedInStream());

또는 타임스탬프가 t인 빈 패킷을 생성해 타임스탬프 경계 t+1을 지정할 수 있습니다.

cc->Outputs.Tag("OUT").Add(Packet(), t);

입력 스트림의 타임스탬프 경계는 패킷 또는 입력 스트림 빈 패킷으로 표시됩니다.

Timestamp bound = cc->Inputs().Tag("IN").Value().Timestamp();

2. TimestampOffset() 입력 스트림에서 출력 스트림으로 바인딩된 타임스탬프를 자동으로 복사하기 위해 지정할 수 있습니다.

cc->SetTimestampOffset(0);

3. ProcessTimestampBounds() 는 각각 새로운 정착된 타임스탬프 (현재 타임스탬프 경계 아래 새로운 최고 타임스태믚)에 대해 Calculator::Process를 호출하기 위해 지정할 수 있습니다. ProcessTimestampBoudns() 가 없으면 Calculator::Process는 하나 이상의 도착 패킷으로만 호출됩니다.

cc->SetProcessTimestampBounds(true);

이 설정을 사용하면 입력 타임스탬프만 업데이트된 경우에도 Calculator가 자체 타임스탬프 경계 계산 및 전파를 수행할 수 있습니다. TimestampOffset()의 효과를 복제하는 데 사용할 수 있지만 추가 요소를 고려하는 타임스탬프 경계를 계산하는 데 사용할 수도 있습니다.

예를 들어, SetTimestampOffset(0)을 복제하기 위해 Calculator는 다음을 수행할 수 있습니다.

absl::Status Open(CalculatorContext* cc) {
  cc->SetProcessTimestampBounds(true);
}

absl::Status Process(CalculatorContext* cc) {
  cc->Outputs.Tag("OUT").SetNextTimestampBound(
      cc->InputTimestamp().NextAllowedInStream());
}

---

Scheduling of Calculator::Open and Calculator::Close

Calculator::Open은 필요한 모든 사이드 패킷이 생성되면 호출됩니다. 입력 사이드 패킷은 인클로징 어플리케이션 또는 그래프 내부의 사이드 패킷 Calculator 에서 제공할 수 있습니다.
API의 CalculatorGraph::Initialize 및 CalculatorGraph::StartRun을 사용해 그래프 외부에서 사이드 패킷을 지정할 수 있습니다.
CalculatorGraphConfig::OutputSidePackets 및 OutputSidePacket::Set을 사용해 그래프 내 Calculator에서 사이드 패킷을 지정할 수 있습니다.

CalculatorGraph::Close는 모든 입력 스트림이 닫히거나 타임스탬프 바운드 Timestamp::Done에 도달하여 Done이 되면 호출됩니다.

참고 : 그래프가 보류 중인 모든 Calculator 실행을 완료하고 완료되면 일부 스트림이 완료되기 전에 MediaPipe가 Calculator::Close에 대한 나머지 호출을 호출해 모든 Calculator가 최종 출력을 생성할 수 있도록 합니다.

TimestampOffset을 사용하면 Calculator::Close에 몇 가지 의미가 생깁니다. SetTimestampOffset(0)을 지정하는 Calculator는 모든 입력 스트림이 Timestamp::Done에 도달했을 때 모든 출력 스트림이 TimeStamp::Done에 도달했음을 신호로 표시하므로 더 이상의 출력이 불가능합니다. 이렇게 하면 이러한 Calculator가 Calculator::Close동안 패킷을 내보내는 것을 방지할 수 있습니다. Calculator가 Calculator::Close 중에 요약 패킷을 생성해야 하는 경우 Calculator::Process는 Calculator::Close 중에 최소한 하나의 타임스탬프를 사용할 수 있도록 타임스탬프 경계를 지정해야 합니다. 즉, 이러한 Calculator는 일반적으로 SetTimestampOffset(0)에 의존할 수 없으며 대신 SetNextTimestampBounds()를 사용해 명시적으로 타임스탬프 경계를 지정해야 합니다.