확률 (probability)
상대 도수에 의한 정의이다.
확률의 고전적 정의
- 표본공간 (sample space)
- 모든 가능한 실험결과들의 집합
- 사건 - 대문자로 표현
- 관심있는 실험결과들의 집합
- 표본 공간의 부분집합
- 어떤 사건이 일어날 확률 - P로 표현
- 표본 공간의 모든 원소가 일어날 확률이 같은 경우
- 사건의 원소의 수 / 표본공간의 원소의 수
- 확률은 0에서 1사이의 값을 가짐
- 1은 무조건 사건이 일어남
- 0은 절대 사건이 일어나지 않음
ex) 주사위를 2번 던졌을 때 합이 10일 확률
표본공간 = { ( 1, 1 ), ( 1, 2 ), ( 1, 3 ), ... , ( 6, 6 ) } 총 36가지
합이 10일 사건 A = { ( 4, 6 ), ( 5, 5 ), ( 6, 4 ) } 총 3가지
확률 P(A) = 3/36 = 1/12
확률의 계산
조합 (combination)이란? 어떤 집합에서 순서에 상관없이 뽑은 원소의 집합
n개 중 r개를 뽑는 조합의 수
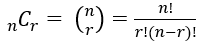
덧셈 법칙 (Addition Law)
- 사건 A나 사건 B가 일어날 확률
- P(A∪B)
- 사건 A와 사건 B가 동시에 일어날 확률
- P(A∩B)
- P(A∪B) = P(A) + P(B) - P(A∩B)
서로 배반 (Mutually Exclusive)
- 두 사건의 교집합이 공집합일 경우 사건 A와 사건 B가 서로 배반한다고 한다.
- P(A∩B) = 0
- P(A∪B) = P(A) + P(B)
조건부 확률 (Conditional probability)
- 어떤 사건 A가 일어났을 때, 다른 사건 B가 일어날 확률
- P(B|A) = P(A∩B)/P(A)
- 단, P(A) > 0
ex) 주사위를 하나 던졌는데, 4이상의 수가 나왔다. 이 때 그 수가 짝수일 확률은?
사건 A : 4 이상의 수가 나오는 확률
사건 B : 짝수가 나오는 사건
P(B|A) = P(A∩B)/P(A) = (1/2) / (1/3) = 2/3
곱셈 법칙 (Multiplication law)
- P(B|A) = P(A∩B)/P(A)
- P(A∩B) = P(B|A)P(A)
ex) 어떤 학교에서 60%의 학생이 남학생이다. 그 학교 남학생의 경우 80%는 축구를 좋아한다. 그 학교에서 학생 1명을 랜덤하게 뽑았을 때 축구를 좋아하는 남학생일 확률은?
P(A∩B) = P(B|A)P(A) = 0.8 * 0.6 = 0.48
서로 독립 (Mutually Independent)
- P(B|A) = P(B)인 경우 사건 A와 B는 서로 독립이라고 한다.
- P(A∩B) = P(B|A)P(A) = P(B)P(A) = P(A)P(B)
여사건
- 사건 A의 여사건
- 사건 A가 일어나지 않을 사건
- A^c로 표시
- 어떤 사건과 그 여사건은 서로 배반이다. 즉, 둘 중 하나는 반드시 일어난다.
- P(A∪A^c) = P(A) + P(A^c) = 1
- P(A) = 1 - P(A^c)
확률의 분할 법칙
그림출처 : 프로그래머스 스쿨

- 사건 B는 다음과 같이 나누어진다.
- B = (A∩B)∪(A^c∩B)
- (A∩B)와 (A^c∩B)는 서로 배반
- ∴ P(B) = P[(A∩B)∪(A^c∩B)] = P(A∩B)∪P(A^c∩B) = P(B|A)P(A) + P(B|A^c)P(A^c)
ex) 어떤 사파리에서 70%가 사자고, 나머지가 호랑이다. 사자는 60%가 2살 이상이고, 호랑이는 40% 정도가 2살 이상이다. 전체 동물 중 2살 이상인 동물의 비율은?
사건 A : 동물이 사자인 사건
사건 B : 동물이 2살 이상인 사건
P(B) = P(B|A)P(A) + P(B|A^c)P(A^c) = 0.6 x 0.7 + 0.4 x 0.3 = 0.54
베이즈 정리
- 처음의 확률
- 사전 확률 (prior probability)
- 수정된 확률
- 사후 확률 (posterior probability)
- P(A|B) = P(A∩B) / P(B) = P(B|A)P(A) / P(B|A)P(A) + P(B|A^c)P(A^c)
ex) 앞 예제에서 동물 한 마리를 랜덤하게 선택했는데, 이 동물이 2살 이었다. 이 동물이 사자일 확률은?
P(A|B) = P(A∩B) / P(B) = P(B|A)P(A) / P(B|A)P(A) + P(B|A^c)P(A^c) = 0.6 x 0.7 / 0.6 x 0.7 + 0.4 x 0.3 = 0.78
그림출처 : 프로그래머스 스쿨

ex) 어떤 사람이 검은색과 흰색의 셔츠를 갖고 있는데, 매일 아침 3/4 정도는 검은색 셔츠를 입고, 1/4 정도는 흰색 셔츠를 입는다. 이 사람이 검은색 셔츠를 입었을 때는 3/4 정도 넥타이를 매고, 흰색 셔츠를 입었을 땐 1/2 정도 넥타이를 맨다 하자. 어느 날 이 사람이 넥타이를 맸다면 이 사람이 검은색 셔츠를 입었을 확률을 구하라.
사건 A : 아침에 검은색 셔츠를 입는 사건 P(A) = 3/4
사건 B : 넥타이를 맨 사건 P(B|A) = 3/4, P(B|A^c) = 1/4
구하는 확률
P(A|B) = (3/4)x(3/4)/(3/4)x(3/4)+(1/2)+(1/4) = 9/11
확률 변수 (random variable)
- 랜덤한 실험 결과에 의존하는 실수. 표본 공간의 부분 집합에 대응하는 실수
- 보통 표본 공간에서 실수로 대응되는 함수로 정의
- 보통 X나 Y 같은 대문자로 표시
이산확률변수 (discrete random variable)
확률변수가 취할 수 있는 모든 수 값들을 하나씩 셀 수 있는 경우
연속확률변수 (continuous random variable)
셀 수 없는 경우
확률 분포 (Probability Distribution)
확률변수가 가질 수 있는 값에 대해 확률을 대응시켜주는 관계
ex) 어떤 확률 변수 X가 가질 수 있는 값 : 0, 1, 2, 3
각 값이 나올 확률
P(X=0) = 0.5
P(X=1) = 0.2
P(X=2) = 0.2
P(X=3) = 0.1
ex) 주사위 2개를 던지는 실험
확률 변수 X : 주사위 숫자의 합
X가 가질 수 있는 값
2, 3, ..., 12
P( X = 12 ) = 1 / 36
확률 변수 Y : 주사위 숫자의 차
Y가 가질 수 있는 값
0, 1, 2, ..., 5
P( Y = 5 ) = 2 / 36 = 1 / 18
확률 변수 X는 주사위를 던질 때마다 값이 달라질 수 있다.
n번 실험하면, n개의 숫자가 나온다. 이 n개의 숫자의 평균과 분산을 계산할 수 있다.
즉, 확률 변수 X도 평균과 분산을 갖는다. 이 평균과 분산을 모집단의 평균과 분산이라 할 수 있다.
확률분포의 표현
표, 그래프, 함수 등 다양하게 표현 가능하다.
이산확률변수
- 이산확률변수의 확률분포는 보통 함수로 주어진다.
- 확률변수 X가 x라는 값을 가질 확률
- P(X = x) = f(x)
- 확률질량함수
- 확률변수 X가 x라는 값을 가질 확률
- 이산확률변수의 평균
- 기대값 (expected value)라고도 한다.
- E(X) = sigma(xP(X=x)x = sigma(xf(x))x
ex) 만약 100,000번의 실험을 했다면,
0이 대략 10,000번 나오고,
2이 대략 30,000번 나오고,
5이 대략 60,000번 나왔다고 하면 평균은
0X10000 + 2X30000 + 5X60000 / 100000 = 3.6
- 이산확률변수의 분산
- 실험을 할 때마다 확률변수의 값은 달라진다. 따라서 그 변동의 정도인 분산을 계산할 수 있다.
- σ^2 = 1/N(N(sigma(x_i-μ)^2)i=1)
- (X - μ)^2의 평균
- σ^2 = E[(X - μ)^2] = (sigma(x - μ)^2)P(X = x) = E(X^2) - {E(X)}^2
- Var(X)라고도 한다.
ex) 위의 예에서의 분산을 구하면
σ^2 = ((0 - 3.6)^2x10,000 + (2 - 3.6)^2x30,000 + (5 - 3.6)^2x60,000)/100,000 = 3.24
결합확률 분포 (Joint probability distribution)
두 개 이상의 확률 변수가 동시에 취하는 값들에 대해 확률을 대응시켜주는 관계
결합확률분포를 통해 각 확률변수의 확률분포를 도출할 수 있다.
=> 주변확률분포 (marginal probability distribution)
공분산 (Covariance)
두 개의 확률변수의 선형 관계를 나타내는 값
Cov(X, Y) -= E[(X - μ_x)(Y - μ_y)] = E(XY) - μ_xμ_y = E[XY] - E[X]E[Y]
상관계수 (correlation coefficient)
공분산은 각 확률 변수의 절대적인 크기에 영향을 받는다. 따라서 단위에 의한 영향을 없앨 필요가 있다.
ρ = Corr(X, Y) = Cov(X, Y)/σ_xσ_y
이항분포
베르누이 시행 (Bernoulli trial)
정확하게 2개의 결과만을 갖는 실험. ex) 동전 던지기
보통 성공과 실패로 결과를 구분하며, 성공의 확률을 p라고 한다.
이항확률변수
확률변수 X는 n번의 베르누이 시행에서 성공의 횟수이다.
이항분포(binomail distribution)
이항확률변수의 확률분포이다.

ex) 어떤 랜덤박스의 뽑기 성공 확률이 0.2이다. 3개를 뽑았을 때, 적어도 하나 이상의 성공이 발생할 확률은?

- 평균
- E(X) = np
- 분산
- Var(X) = np(1-p)
- 표준편차
- SD(X) = root(np(1-p))
정규분포
연속확률 변수의 확률 분포. 확률밀도함수(probability density function)로 표현한다.
P[a ≤ X ≤ b] = b(integral(f(x)dx))a
그래프의 넓이가 확률이 된다.
정규분포의 확률밀도함수

X ~ N (μ, σ^2) => 평균이 μ고, 분산이 σ^2인 정규분포를 따른다는 뜻이다.
표준정규확률변수 (standard normal random variable)
Z = X - μ / σ
표준정규분포 (standard normal distribution)
Z ~ N (0, 1)
표준 정규분포표 => P[Z ≤ z]
ex) X~N(4, 3^2)
P[X ≤ 4]
= P[X - μ / σ ≤ 4 - μ / σ]
= P[Z ≤ 4-4 / 3] = P[Z ≤ 0]
=0.5
ex2)
P[4 ≤ X ≤ 7]
= P[X ≤ 7] + P[X < 4]
= P[Z ≤ 7-4 / 3] - P[Z < 0]
= P[Z ≤ 1 ] - P[Z < 0] = 0.8413 - 0.5 = 0.3413
포아송 분포 (Poisson distribution)
일정한 시간단위 또는 공간 단위에서 발생하는 이벤트의 수의 확률분포
확률분포함수 (확률질량함수)
P[X = x] = f(x) = λ^x(e^-λ / x!), x = 0,1, 2, ...
평균 : λ
분산 : λ
ex) 어느 웹사이트에 시간당 접속자 수는 평균이 3 (λ = 3)인 포아송 분포를 따른다고 할 때, 앞으로 1시간 동안 접속자 수가 2명 이하일 확률은?
P [X ≤ 2] = P [X = 0] + P [X = 1] + P [X = 2] = 3^0(e^-3 / 0!) + 3^1(e^-3 / 1!) + 3^2(e^-3 / 2!)
= 0.04998 + 0.14936 + 0.22404 = 0.42319
지수분포 (Exponential distribution)
포아송 분포에 의해 어떤 사건이 발생할 때, 어느 한 시점으로부터 이 사건이 발생할 때까지 걸리는 시간에 대한 확률 분포
확률밀도 함수
f(t) = λe^(-λt)
λ : 포아송 분포 평균
평균 : E(T) = 1 / λ
분산 : Var(T) = 1 / λ^2
ex) 어느 웹사이트에 시간당 접속자 수는 λ = 3인 포아송 분포를 따른다 한다. 지금부터 시작하여 첫번째 접속자가 30분 이내 올 확률은?
P[T ≤ 0.5] = 0.5(integral(λe^(-λt))0)dt = 0.5(integral(3e^(-3t))0)dt = 0.5([-e^(-3t)])0 = 1-e^(-1.5) = 1-0.2231 = 0.7769
'AI > KDT 인공지능' 카테고리의 다른 글
| [05/04] Python으로 데이터 다루기 - Numpy (0) | 2021.05.04 |
|---|---|
| [05/03] 인공지능 수학 - 추정, 검정, 엔트로피 (0) | 2021.05.03 |
| [04/28] 인공지능 수학 - 자료의 정리 (0) | 2021.04.28 |
| [04/27] 인공지능 수학 - 미적분 (0) | 2021.04.27 |
| [04/26] 인공지능 수학 - 가우스 소거법 (0) | 2021.04.27 |