Mnist 데이터 분류
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Scikit-Learn ≥0.20 is required
import sklearn
assert sklearn.__version__ >= "0.20"
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "classification"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)MNIST 데이터를 불러오고, 확인해보자.
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1, cache=True)
mnist.keys()
X, y = mnist["data"], mnist["target"]
print(X.shape) # (70000, 784)%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
some_digit = X[2]
some_digit_image = some_digit.reshape(28, 28)
plt.imshow(some_digit_image, cmap=mpl.cm.binary)
plt.axis("off")
save_fig("some_digit_plot")
plt.show()
some_digit에는 검은 부분을 제외하고 전부 0인 배열이 나타나게 된다.
y = y.astype(np.uint8)def plot_digit(data):
image = data.reshape(28, 28)
plt.imshow(image, cmap = mpl.cm.binary,
interpolation="nearest")
plt.axis("off")
def plot_digits(instances, images_per_row=10, **options):
size = 28
images_per_row = min(len(instances), images_per_row)
images = [instance.reshape(size,size) for instance in instances]
n_rows = (len(instances) - 1) // images_per_row + 1
row_images = []
n_empty = n_rows * images_per_row - len(instances)
images.append(np.zeros((size, size * n_empty)))
for row in range(n_rows):
rimages = images[row * images_per_row : (row + 1) * images_per_row]
row_images.append(np.concatenate(rimages, axis=1))
image = np.concatenate(row_images, axis=0)
plt.imshow(image, cmap = mpl.cm.binary, **options)
plt.axis("off")plt.figure(figsize=(9,9))
example_images = X[:100]
plot_digits(example_images, images_per_row=10)
save_fig("more_digits_plot")
plt.show()
학습 데이터와 테스트 데이터를 분류하자.
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]이진분류기 (Binary classifier)
숫자 5만 식별해보자.
y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)
# 로지스틱 회귀 모델 사용
from sklearn.linear_model import LogisticRegression
log_clf = LogisticRegression(random_state=0).fit(X_train, y_train_5)
log_clf.predict([X[0],X[1],X[2]]) # array([ True, False, False]) #y[0]=5, y[1]=0, y[2]=4이기 때문에 제대로 정답이 나왔다.
# 교차 검증을 사용해 평가
from sklearn.model_selection import cross_val_score
cross_val_score(log_clf, X_train, y_train_5, cv=3, scoring="accuracy") # array([0.97525, 0.97325, 0.9732 ])모든 교차 검증 폴드에 대해 정확도가 97% 이상이다. 모델이 좋은 것일까?
또 다른 classify를 만들어 보도록 하자. 지금 만들 분류기는 무조건 5가 아니라고 판별하는 함수이다.
from sklearn.base import BaseEstimator
class Never5Classifier(BaseEstimator):
def fit(self, X, y=None):
pass
def predict(self, X):
return np.zeros(len(X), dtype=bool)
never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train, y_train_5, cv=3, scoring="accuracy") # array([0.91125, 0.90855, 0.90915])
never_5_clf.predict(X) # array([False, False, False, ..., False, False, False])다 5가 아니라고 판별하는 데에도 불구하고 정확도가 90이 넘게 나온다. 어떻게 이런 결과가 나오는 것일까?
숫자 5는 학습 데이터 상에서 10퍼센트 정도의 분포를 차지한다. 그래서 무조건 이것은 5가 아니라고 하면 맞을 확률이 자연스럽게 90퍼센트가 넘게 되는 것이다.
이와 비슷한 경우로 1%의 사람에게서만 발병되는 아주 희귀한 병에 대해서 진단을 할 때 관련 모델을 만들면 그 모델이 100%에 대해 그 병이 아니다라고 진단을 내리게 되면 그 진단의 Accuracy는 99%가 되나, 그 모델은 좋은 모델이라고 할 수 없는 것이다. 왜냐하면 그 병을 지닌 사람에 대해서 정확한 진단을 내릴 수 없게 되기 때문이다.
즉, 목표값이 불균형인 경우에 정확도는 좋은 지표가 아니다.
오차 행렬(Confusion matrix)
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(log_clf, X_train, y_train_5, cv=3)
y_train_pred.shape # (60000, )
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred)
'''
array([[54039, 540],
[ 1026, 4395]], dtype=int64)
'''TN|FP
FN|TP
로 구성되어 있는 오차 행렬이다.

이 때 정밀도는
Precision = TP/TP+FP
재현율은
Recall = TP/TP+FN
이다.
즉, 위와 같은 경우에서의 정밀도는
4395/(4395+540)
재현율은
4395/(4395+1026)
scikit-learn에서 주어진 함수를 통해 정밀도, 재현율을 구해보자.
from sklearn.metrics import precision_score, recall_score
precision_score(y_train_5, y_train_pred) # 0.8905775075987842
4395/(4395+541) # 0.8903970826580226
recall_score(y_train_5, y_train_pred) # 0.8107360265633647
4395/(4395+1026) # 0.8107360265633647
그렇다면 모든 답을 5가 아니라고 판별한 모델에 대한 오차 행렬을 구해보자.
confusion_matrix(y_train_5, never_5_clf.predict(X)[:60000])
'''
array([[54579, 0],
[ 5421, 0]], dtype=int64)
'''
precision_score(y_train_5, never_5_clf.predict(X)[:60000]) # 0
recall_score(y_train_5, never_5_clf.predict(X)[:60000]) # 0positive 쪽의 답이 전부 0이 나왔다. 그에 따라 자연스럽게 정밀도와 재현율 또한 0이 나오게 된다. 정확도는 90퍼센트로 높게 나왔지만 결과적으론 상당히 좋지 않은 모델이 된 것이다.
그렇다면 어떤 경우에 정밀도가 중요하고, 어떤 경우에 재현율이 중요할까?
병에 대한 진단 모델같은 큰 Risk가 있는 모델의 경우 정밀도보다는 재현율이 높아야 한다.
반대의 경우로, 동영상을 분류할 때 어린이들에게 안전한 동영상인지 아닌지 판별하는 알고리즘을 만든다고 할 땐 정밀도가 중요하다고 할 수 있다.
Precision / Recall Trade-off

threshold를 어디에 잡는지에 따라 Precision과 Recall의 값이 완전히 달라질 것이다.
y_train_pred[48], y_train_5[48] # (True, False)
some_digit = X_train[48]
y_scores = log_clf.decision_function([some_digit]) # 예측값이 얼마나 정답으로부터 떨어져 있는지 수치로 보여줌.
y_scores # array([0.22419046])some_digit_image = some_digit.reshape(28, 28)
plt.imshow(some_digit_image, cmap=mpl.cm.binary)
plt.axis("off")
save_fig("some_digit_plot")
plt.show()
threshold = 0
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred # array([ True])
threshold = 0.5
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred # array([False]) 한 경우에 대해 threshold에 따라서 recall을 줄일 수도 (threshold가 클수록) 있다. 이런 식으로 recall과 precision의 비율을 조절할 수 있는 것이다.
y_scores = cross_val_predict(log_clf, X_train, y_train_5, cv=3,
method="decision_function")
y_scores.shape # (60000,)
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
precisions.shape # (59897,) # 각 threshold에 따른 precision의 값들
thresholds.shape # (59896,) # 가능한 모든 경우의 threshold의 값들
precision과 recall을 그래프로 나타낼 수 있다.
def plot_precision_vs_recall(precisions, recalls):
plt.plot(recalls, precisions, "b-", linewidth=2)
plt.xlabel("Recall", fontsize=16)
plt.ylabel("Precision", fontsize=16)
plt.axis([0, 1, 0, 1])
plt.grid(True)
plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
save_fig("precision_vs_recall_plot")
plt.show()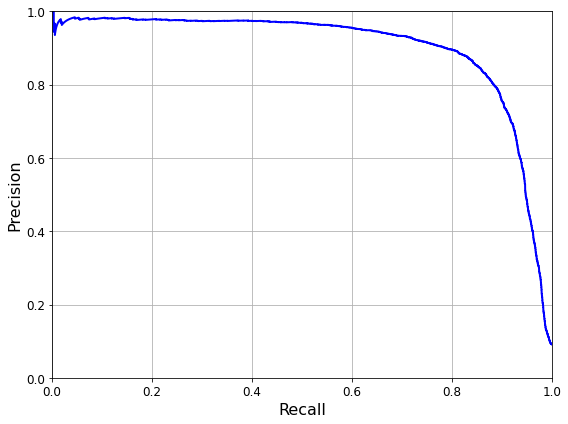
다중 분류 (Multicalss Classification)
지금까지 MNIST 문제를 이진 분류해보았다. 이번엔 원래의 MNIST 분류 문제의 목적에 맞게 다중 분류를 해보도록 하자.
from sklearn.linear_model import LogisticRegression
softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10) # multinomial로 설정하면 multiclass에 대한 logisticregression이 가능
softmax_reg.fit(X_train, y_train)
softmax_reg.predict(X_train)[:10] # array([5, 0, 4, 1, 9, 2, 1, 3, 1, 4], dtype=uint8) # 정확히 예측하고 있다.
from sklearn.metrics import accuracy_score
y_pred = softmax_reg.predict(X_test)
accuracy_score(y_test, y_pred) # 0.9243
위의 모델을 조금 더 향상시키도록 하자.
Data Augmentation
가지고 있는 학습데이터에 레이블을 유지한 채 약간의 변형을 가해 데이터를 더하여 모델을 새로 학습했을 때 조금 더 안정적인 모델을 만들어낼 수 있을 것이다.
from scipy.ndimage.interpolation import shift
# 오른쪽이나 아래로 이미지를 조금씩 shift시키는 함수
def shift_image(image, dx, dy):
image = image.reshape((28, 28))
shifted_image = shift(image, [dy, dx], cval=0, mode="constant")
return shifted_image.reshape([-1])
image = X_train[1000]
shifted_image_down = shift_image(image, 0, 5) # 아래쪽으로 이동
shifted_image_left = shift_image(image, -5, 0) # 왼쪽으로 이동
plt.figure(figsize=(12,3))
plt.subplot(131)
plt.title("Original", fontsize=14)
plt.imshow(image.reshape(28, 28), interpolation="nearest", cmap="Greys")
plt.subplot(132)
plt.title("Shifted down", fontsize=14)
plt.imshow(shifted_image_down.reshape(28, 28), interpolation="nearest", cmap="Greys")
plt.subplot(133)
plt.title("Shifted left", fontsize=14)
plt.imshow(shifted_image_left.reshape(28, 28), interpolation="nearest", cmap="Greys")
plt.show()
X_train_augmented = [image for image in X_train]
y_train_augmented = [label for label in y_train]
# 레이블을 유지한 채 shift한 데이터를 추가하는 작업
for dx, dy in ((1, 0), (-1, 0), (0, 1), (0, -1)):
for image, label in zip(X_train, y_train):
X_train_augmented.append(shift_image(image, dx, dy))
y_train_augmented.append(label)
X_train_augmented = np.array(X_train_augmented)
y_train_augmented = np.array(y_train_augmented)
X_train_augmented.shape # (300000, 784) # 원래의 데이터보다 5배만큼 늘어났다.
# 같은 레이블의 데이터가 연속으로 있으면 모델을 학습하는 데 있어서 좋지 않은 영향을 끼칠 것이다. 그래서 데이터를 섞어주는 작업을 하자.
shuffle_idx = np.random.permutation(len(X_train_augmented))
X_train_augmented = X_train_augmented[shuffle_idx]
y_train_augmented = y_train_augmented[shuffle_idx]
# 모델 학습
softmax_reg_augmented = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10)
softmax_reg_augmented.fit(X_train_augmented, y_train_augmented)
y_pred = softmax_reg_augmented.predict(X_test)
accuracy_score(y_test, y_pred) # 0.9279 # data augmentation을 진행하기 전보다 0.002정도 오른 것을 확인할 수 있다.
# 0.002면 작은 수치일 수도 있으나, 이미 잘 나온 모델에서 조금이라도 정확도를 올렸다는 것은 굉장히 유의미한 일이다.Titanic 데이터셋에 대해 분류하기
import numpy as np
import pandas as pd
train_data = pd.read_csv("titanic.csv")
속성들
- Survived: that's the target, 0 means the passenger did not survive, while 1 means he/she survived.
- Pclass: passenger class.
- Name, Sex, Age: self-explanatory
- SibSp: how many siblings & spouses of the passenger aboard the Titanic.
- Parch: how many children & parents of the passenger aboard the Titanic.
- Ticket: ticket id
- Fare: price paid (in pounds)
- Cabin: passenger's cabin number
- Embarked: where the passenger embarked the Titanic
train_data.info()
'''
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 PassengerId 891 non-null int64
1 Survived 891 non-null int64
2 Pclass 891 non-null int64
3 Name 891 non-null object
4 Sex 891 non-null object
5 Age 714 non-null float64
6 SibSp 891 non-null int64
7 Parch 891 non-null int64
8 Ticket 891 non-null object
9 Fare 891 non-null float64
10 Cabin 204 non-null object
11 Embarked 889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.7+ KB
'''Age, Cabin, Embarked 속성들이 missing value를 갖고 있다.
Cabin, Name, Ticket 속성은 무시하도록 하자.
이 중 Ticket같은 경우는 고유한 번호가 될 가능성이 높은데 고유한 식별자를 feature data로 쓰면 학습을 할 때 고유한 정보를 외우는 수준까지 갈 수도 있기 때문에(이 고유한 식별자에 집중하게 될 수도 있기 때문에) 예측값이 굉장히 안 좋아질 수도 있다. 그렇기 때문에 사용하지 않는 것이 더 좋다고 볼 수 있다.
train_data["Survived"].value_counts()
'''
0 549
1 342
Name: Survived, dtype: int64
'''
train_data["Pclass"].value_counts()
'''
3 491
1 216
2 184
Name: Pclass, dtype: int64
'''
train_data["Sex"].value_counts()
'''
male 577
female 314
Name: Sex, dtype: int64
'''
train_data["Embarked"].value_counts()
'''
S 644
C 168
Q 77
Name: Embarked, dtype: int64
'''from sklearn.base import BaseEstimator, TransformerMixin
# 속성을 골라 사용할 수 있도록 해줌
class DataFrameSelector(BaseEstimator, TransformerMixin):
def __init__(self, attribute_names):
self.attribute_names = attribute_names
def fit(self, X, y=None):
return self
def transform(self, X):
return X[self.attribute_names]
# Numerical 속성 처리 Pipeline
from sklearn.pipeline import Pipeline
from sklearn.impute import SimpleImputer
num_pipeline = Pipeline([
("select_numeric", DataFrameSelector(["Age", "SibSp", "Parch", "Fare"])),
("imputer", SimpleImputer(strategy="median")),
])
# missing value를 가장 많이 나오는 값으로 채워넣어준다.
class MostFrequentImputer(BaseEstimator, TransformerMixin):
def fit(self, X, y=None):
self.most_frequent_ = pd.Series([X[c].value_counts().index[0] for c in X],
index=X.columns)
return self
def transform(self, X, y=None):
return X.fillna(self.most_frequent_)
# Categorical 속성 처리 Pipeline
from sklearn.preprocessing import OneHotEncoder
cat_pipeline = Pipeline([
("select_cat", DataFrameSelector(["Pclass", "Sex", "Embarked"])),
("imputer", MostFrequentImputer()),
("cat_encoder", OneHotEncoder(sparse=False)),
])
# Categorical, Numerical 속성들을 통합하자.
from sklearn.pipeline import FeatureUnion
preprocess_pipeline = FeatureUnion(transformer_list=[
("num_pipeline", num_pipeline),
("cat_pipeline", cat_pipeline),
])
# 최종적으로 만들어진 pipeline을 train_data에 적용시켜보자.
X_train = preprocess_pipeline.fit_transform(train_data)
X_train.shape # (891, 12)
# 목표값 벡터
y_train = train_data["Survived"]
log_clf = LogisticRegression(random_state=0).fit(X_train, y_train)
# 모델에서 어떤 통찰을 얻을 수 있는지 살펴보기
a = np.c_[log_clf.decision_function(X_train), y_train, X_train] # np.c_는 1차원 배열을 칼럼으로 붙여 2차원 배열로 만드는 것이다.
df = pd.DataFrame(data=a, columns=["Score", "Survived", "Age", "SibSp", "Parch", "Fare", "Pclass_1", "Pclass_2", "Pclass_3", "Female", "Male", "Embarked_C", "Embarked_Q", "Embarked_S"])df.sort_values(by=['Score'], ascending=False)[:20]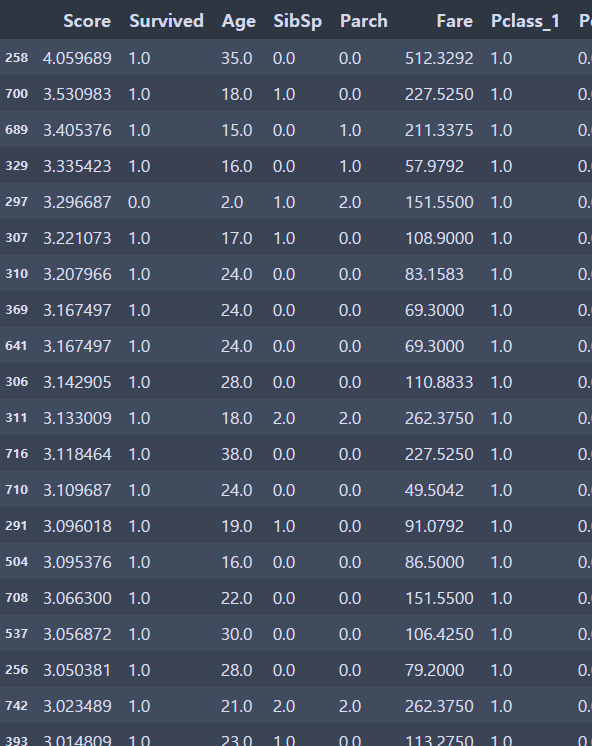
df.sort_values(by=['Score'])[:20]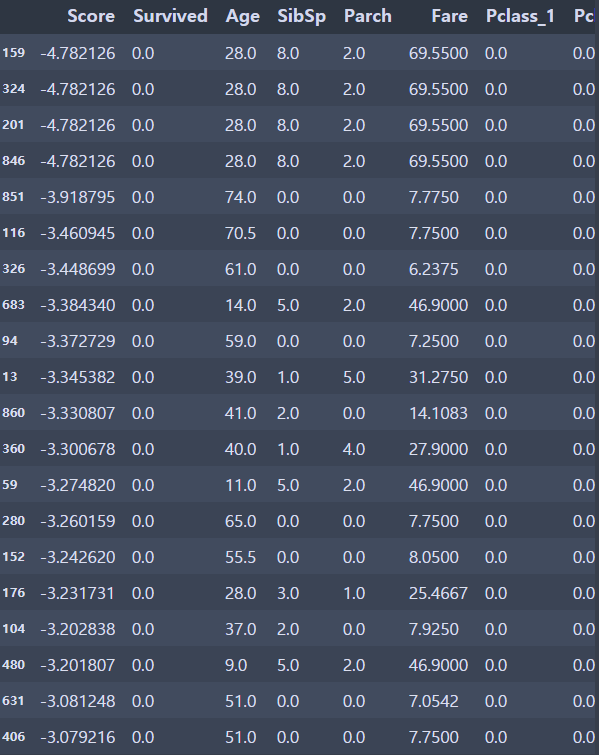
'AI > KDT 인공지능' 카테고리의 다른 글
| [06/21] 신경망의 기초 (0) | 2021.06.21 |
|---|---|
| [06/16] 인공지능과 기계학습 (0) | 2021.06.16 |
| 오토인코더, t-SNE (0) | 2021.06.14 |
| [06/02] End to End Machine Learning Project (0) | 2021.06.02 |
| [05/18] Django로 동적 웹페이지 만들기 (0) | 2021.05.18 |