누런강냉이

Git

분산 버전관리 시스템이다.

git 설치 링크 : git-scm.com/

해당 운영체제에 맞는 Git을 설치하면 된다.

Git 시작하기

• git init
  • 로컬 저장소 생성
  • 현재 작업중인 디렉토리를 git 저장소로 지정할 수 있다.

vim을 통해 initialize한 저장소에 "Hello World!"문을 출력하는 example.py 파일을 생성한다.

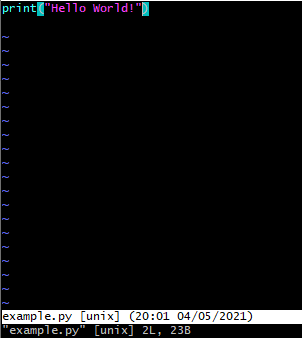
• git status
  • git 저장소의 상태를 확인하는 것

example.py 파일은 다음 commit에 반영이 안 된다는 문구가 나오게 된다. 이 파일을 커밋에 반영할 파일로 지정해보자.

• git add
  • 다음에 commit을 무엇을 남길지 지정하는 행위

example.py 파일을 unstaged 상태에서 staged 상태로 바꾼다.

즉, example.py을 다음 commit에 넣겠다 선언하는 것이다.

• git commit
  • add된 것들을 다음 commit으로서, snapshot으로 남긴다

snapshot에 대한 메세지를 담아 commit한다. 메세지를 담으려면 git commit 뒤에 -m을 붙이고 남길 메세지를 작성하면 된다.

• git log
  • commit을 확인한다.

Git의 Branch

코드의 흐름을 분산, 가지치기 하여 각각 독립적인 환경에서 코드를 수정해나갈 수 있도록 해주는 것이 Branch이다. 

• git branch <branch_name>
  • git branch를 생성하는 명령어이다.
  • branch를 생성하기 전에는 Default로 master라는 branch가 기본적으로 생성된다.

이전과 다르게 master와 develop이라는 두 개의 branch가 있는 것을 확인할 수 있다.

• git checkout <branch_name>
  • branch_name의 branch로 전환해주는 명령어이다.

현재 branch가 develop을 가리키고 있음을 확인할 수 있다.

이 전환된 branch 상태에서 example.py 파일에 변화를 줘보자.

"Hello World in Develop branch!"라는 문장을 example.py에 추가했다.

그 후 상태를 확인하면

다음과 같이 변경 사항이 commit에 반영되지 않았다는 상태를 확인할 수 있다.

이 example.py를 commit하도록 하자.

master branch에서 작업한 commit 내역과 develop branch에서 작업한 commit 내역이 따로 저장되어 있는 것을 확인할 수 있다. 다시 master branch로 돌아가게 된다면 이 example.py는 어떻게 되어 있을까?

develop branch에서 작업한 변경 사항이 master branch에는 반영되어 있지 않은 것을 확인할 수 있다.

이 때 master branch가 중심 branch이기 때문에

develop의 변경 사항을 master에도 병합을 해야 할 때가 있을텐데 그렇게 하려면 어떻게 해야 할까?

• git merge <branch_name>
  • 현재 작업중인 Branch를 원하는 Branch에 병합할 수 있다.

develop과 master가 같은 commit을 가지게 되는 것을 확인할 수 있다.

실제로 exmaple.py 파일을 확인해보면 develop branch에서 변경했던 사항이 master branch에도 잘 반영되어 있는 것을 확인할 수 있다. 이를 통해 Fast forward 방식의 merge가 잘 이루어졌음을 알 수 있다. 이외에도 merge 방식은 다양한 방식이 있다.

• git branch -d <branch_name>
  • branch를 삭제하는 명령어이다.

branch가 잘 삭제되었음을 확인할 수 있다.

Github

지금까지 살펴봤던 git은 로컬 저장소고 원격 저장소는 이 git과 상호작용하면서 분산 시스템을 구축하게 된다.

다양한 원격 저장소가 있지만 그 중 Github를 사용해보도록 하겠다.

github의 계정을 생성했으면 다음과 같이 new repository를 생성한다.

생성했으면 로컬 저장소와 원격 저장소를 연결해주도록 하자.

• git remote add <별칭> <원격 저장소 주소>
  
  • 로컬 저장소와 원격 저장소를 연결해주는 명령어이다.

이렇게 연결해주면 원격 저장소에 로컬 저장소에서 작업하고 있던 정보들을 전달해줄 수 있다. 그 전에 github에서는 중심 branch의 이름을 main이라는 이름으로 사용하기 때문에 git의 master branch의 이름을 다음과 같이 main으로 변경해주어야 한다.

• git push <remote_repo_name> <branch_name>
  • 로컬 저장소에서 작업하고 있던 정보들을 원격 저장소에 반영하는 명령어이다.

push가 이뤄지고 난 후 연결한 원격 저장소로 가보면

다음과 같이 변경사항이 잘 반영되었음을 확인할 수 있다.

github 원격 저장소 우상단에 있는 Fork를 하면 다른 사람의 원격 저장소를 자신의 원격 저장소로 복사 - 붙여넣기 할 수 있다.

이 원격 저장소에 있는 내용을 바탕으로 로컬 저장소에서 작업을 진행해보도록 하자.

• git clone <remote_repo><alias>

다음과 같이 git clone을 통해 원격 저장소에 있는 material을 로컬 저장소로 가져올 수 있게 된다.

Numpy 

Array의 Indexing와 Array의 Slicing

Python의 List와 유사하게 진행한다.

Array의 Broadcasting

Numpy가 연산을 진행하는 특수한 방법이다.

1. M x N, M x 1
   • M x 1 부분을 N만큼 똑같이 복제해서 계산한다.
2. M x N, 1 x N
   • 1 x N 부분을 M만큼 똑같이 복제해서 계산한다.
3. M x 1, 1 x N
   • 서로 보완하는 구조로 M x 1 부분은 N만큼, 1 x N 부분은 M만큼 복제해서 계산하여 M x N 구조의 Array가 결과물로 출력된다.

영벡터를 numpy로 선언

영벡터 = 원소가 모두 0인 벡터(행렬)

np.zeros(dim)을 통해 생성한다.

일벡터(일행렬)을 numpy로 선언

일벡터 = 원소가 모두 1인 벡터(해열)

np.ones(dim)을 통해 생성

대각행렬 (diagonal matrix)

Main diagonal을 제외한 성분이 0인 행렬

np.diag(main_diagonal)을 통해 생성

항등행렬 (identity matrix)

Main diagonal이 1인 대각행렬

np.eye()를 사용

행렬곱 (dot product)

행렬간의 곱연산

np.dot or @ 사용

Linear Algebra with Numpy

트레이스 (trace)

Main diagonal의 합

np.trace()를 사용

행렬식 (determinant)

행렬을 대표하는 값들 중 하나 => 선형변환

ex)

1 4 7

2 5 8

3 6 9

=> 

1(5 * 9 - 6 * 8) - 4(2 * 9 - 3 * 8) + 7(2 * 6 - 3 * 5) = - 3 + 24 - 21 = 0

Full rank가 아니다. 즉, 선형변환 과정에서 차원의 손실이 일어난다.

선형변환을 통해 insight를 얻을 수 있다!

np.linalg.det()으로 계산

역행렬

행렬 A에 대해 AB = BA = 1을 만족하는 행렬 B = A^-1

np.linalg.inv()으로 계산

고유값과 고유벡터 (eigenvalue and eigenvector)

 Ax = λx가 있을 때 이 등식을 만족시키는 λ값과 이에 대응하는 x를 각각 고유값과 고유벡터라고 한다.

np.linalg.eig()으로 계산.

이 때 결과는 column을 기준으로 eigenvector가 된다.

표본분포

• 통계적 추론
  • 표본 조사를 통해 모집단에 대한 해석을 진행
  • 전수조사는 실질적으로 불가능한 경우가 많다.
• 표본 조사는 반드시 오차가 발생
  •  표본과 모집단과의 관계를 이해해야 한다.
  • 적절한 표본 추출 방법이 필요하다.
    • 단순 랜덤 추출법 (random sampling)
    • 난수표 사용
    • 랜덤넘버 생성기 사용 https://colab.research.google.com

• 표본 조사를 통해 파악하고자 하는 정보
  • 모수 (Parameter)
• 모수의 종류
  • 모평균, 모분산, 모비율 등
  • 모수를 추정하기 위해 표본을 선택해 표본 평균이나 표본 분산 등 계산
• 통계량 (statistic)
  • 표본 평균이나 표본 분산과 같은 표본의 특성값
  • 표본 평균이 가질 수 있는 값도 하나의 확률분포를 갖는다. => 표본분포 (sampling distribution)
• 표본 평균
  • 모평균을 알아내는데 쓰이는 통계량
• 표본 평균의 분포
  • x_1, x_2, ... , x_n
    • 평균 : μ, 분산 : σ^2
  • 표본평균
    • xbar = 1/n(n(sigma(x_i)i)
    • Xbar ~ N ( μ, σ^2/n )

중심극한정리(central limit theorem)

• 정규모집단에서 추출된 표본의 측정값
• 표본평균
  • xbar = 1/n(n(sigma(x_i)i))
  • n이 충분히 큰 경우 (n ≥ 30)
    • 근사적으로 Xbar ~ N (μ, σ^2/n ) => 근사적으로 정규분포를 따른다!

모평균의 추정

표본평균의 특성

• 모집단이 정규분포인 경우
  • 표본평균 사용
  • xbar = 1/n(n(sigma(x_i)i))

• 대표본인 경우 (N>=30)
  • 중심극한 정리에 의해 표본평균이 정규분포를 따른다 가정
• 점추정
  • 표본평균이 점 추정값 (추정량)이 된다.
• 구간추정
  • 모평균 μ의 100(1-a)% 신뢰구간 (confidnece interval)
    • (μ 추정량) ± z_(a/z)(추정량의 표준편차)
    • 정규분포에서 σ를 알 때, (xbar - z_(alpha/z)σ / root(n), xbar + z_(a/z)σ / root(n)) (알파는 0.? 이런 값들을 나타낼 때 주로 사용)
    • 실용적이지 못하다. 대부분의 경우는 정규분포가 아니거나 표준편차가 알려져 있지 않기 때문에...
  • 표본의 크기가 클 때 중심극한 정리 사용
    • (μ의 추정량) ± z_(alpha/z)(추정량의 표준편차)
    • (xbar - z_(a/2)s / root(n), xbar + z_(a/2)s / root(n))
  • ex) 어떤 학교의 고1 남학생의 평균키를 추정하기 위해 36명을 표본으로 추출하여 그 표본평균과 표본표준편차를 계산해 그 결과가 아래와 같다.
    • xbar = 173.6, s = 3.6
    • 평균키에 대한 95% 신뢰 구간을 구하시오.
      • a = 0.05
      • z_(a/2) = z_0.025 = 1.96
      • z_(a/2)s / root(n) = 1.96 x 3.6 / root(36) = 1.98 x 3.6 / 6 = 1.176
      • 95% 신뢰구간 = (173.6 - 1.176, 173.6 + 1.176) = (172.4, 174.8)

모비율의 추정

• 점 추정
  • 확률변수 X 
    • n개의 표본에서 특정 속성을 갖는 표본의 개수
  • 모비율 p의 점추정량
    • phat = X / n
  • ex) 대학교 1학년생의 흡연율을 조사하기 위해 150명을 랜덤하게 선택하여 흡연여부를 조사했다. 이 중 48명이 흡연을 하고 있다. 이 대학교 1학년생의 흡연율의 평균을 점추정하시오.
    • n = 150, X = 48
    • phat = X / n = 48 / 150 = 0.32
• 구간 추정
  • n이 충분히 클 때
    • nphat > 5, n(1-phat) > 5일 때를 의미
    • X~N(np, np(1-p))
  • 확률변수 X의 표준화
    • Z = X - np / root(nphat(1-phat)) = phat - p / root(phat(1-phat)/n)
    • 근사적으로 표준정규분포 N(0, 1)를 따름
  • P(|Z| ≤ z_(a/z) = 1- alpha
    • P(-z_(alpha/2) ≤ Z ≤ z_(alpha/2)) = P(-z_(alpha/2) ≤ phat-p/root(phat(1-phat)/n) = 1 - alpha
  • 모비율 p의 100(1 - alpha)% 신뢰구간 (confidence interval)
    • (phat - z_(a/2)root(phat(1-phat)/n, phat + z_(a/2)root(phat(1-phat)n))
  • ex) 대학교 1학년생의 흡연율을 조사하기 위해 150명을 랜덤하게 선택하여 흡연여부를 조사하였다. 이 중 48명이 흡연을 하고 있었다. 이 때, 흡연율 p의 95% 신뢰구간 (confidence interval)을 구하시오.
    • alpha = 0.05, z_(alpha/2) = z_0.025 = 1.96, phat = 0.32
    • root(phat(1-phat)/n) = root((0.32)(0.68)/150) = 0.038

검정

통계적 가설 검정

• 가설 검정
  • 가설의 주장을 검증하는 것
  • 표본평균 Xbar가 μ_0보다 얼마나 커야 모평균 μ가 μ_0보다 크다고 할 수 있을 것인가?
    • 표본평균은 표본의 선택에 의해 달라진다!
  • 귀무가설 H_0 : μ = μ_0
    • 귀무가설을 기각하기 위해선 Xbar가 큰 값이 나와야 한다.
      • 귀무가설을 참이라 가정할 때, 랜덤하게 선택한 표본에서 지금의 Xbar가 나올 확률을 계산할 필요가 있다. 이 때, 확률이 낮다면 귀무가설이 참이 아니라고 판단한다.
    • 대립가설 H_1 : μ > μ_0
  • 확률이 낮다는 기준점이 필요하기 때문에 유의수준 alpha를 도입한다.
  • P(Xbar ≥ k) ≤ alpha가 되는 k를 찾아야 한다.
  • 표준정규확률변수로 변환한 것을 검정통계량이라고 한다.
    • Z = Xbar - μ / (S / root(n)) ~ N(0, 1)
    • P(Z ≥ z_alpha) = alpha
  • 따라서 Xbar를 Z로 변환한 후 Z값이 z_alpha보다 큰지 검토
    • 크다면 귀무가설을 기각하고, 그렇지 않다면 귀무가설을 채택한다.
  • 검정의 단계
    • H_0, H_1 설정
    • 우의수준 alpha 설정
    • 검정통계량 계산
    • 기각역 또는 임계값 계산
    • 주어진 데이터로부터 유의성 판정

• 대립가설
  • 문제에서 검정하고자 하는 것이 무엇인지 파악이 필요하다.
    • 대립가설 H_1 채택을 위한 통계적 증거 확보가 필요하다.
    • 증거가 없으면 귀무가설 H_0를 채택한다.
    • H_1 : μ > μ_0 
    • H_1 : μ > μ_0
    • H_1 : μ ≠ μ_0
• 검정통계량
  • n ≥ 30인 경우
    • 중심극한 정리 사용
    • Z = Xbar - μ / (s / root(n)) ~ N(0, 1)
  • 모집단이 정규 모집단이고, 모표준편차 σ가 주어진 경우
    • Z = Xbar - μ / (σ / root(n)) ~ N(0, 1)

엔트로피 (Entropy)

• 자기정보 (Self-information)
  • i(A) = log_b(1 / P(A)) = -log_bP(A)
    • A : 사건
  • 확률이 높은 사건은 정보가 많지 않다.
  • 정보의 단위
    • b = 2 : bits
    • b = e : nets
    • b = 10 : hartleys
  • 특성
    • i(AB) = log_b(1 / P(A)P(B)) = log_b(1 / P(A)) + log_b(1 / P(B)) = i(A) + i(B)
  • P(H) = 1/8, P(T) = 7/8
    • i(H) = 3비트, i(T) = 0.193비트
• 엔트로피
  • 자기 정보의 평균
    • H(X) = sigma(P(A_j)i(A_j))j = -sigma(P(A_j)((log_2)P)(A_j))j
  • 특성
    • 0 ≤ H(X) ≤ ((log_2)K)
      • K : 사건의 수
  • 활용
    • 평균비트수 표현
    • 데이터 압축에 사용
  • 4가지 정보를 표현하는데 필요한 비트수는 일반적으로 2비트
  • i(X)를 활용하는 경우
    • 평균비트수
      • 1 x 1/2 + 2 x 1/4 + 3 x 1/8 + 3 x 1/8 = 14/8 = 7/4 비트
• 교차 엔트로피
  • 확률분포 P와 Q
    • S = { A_j }
      • P(A_j) : 확률분포 P에서 사건 A_j가 발생할 확률
      • Q(A_j) : 확률분포 Q에서 사건 A_j가 발생할 확률
      • i(A_j) : 확률분포 Q에서 사건 A_j의 자기정보
        • i(A_j) = -(log_2)Q(A_j)
        • 자기 정보는 A_j를 표현하는 비트수이다.
        • 잘못된 확률분포 Q를 사용하게 되면, 실제 최적 비트수를 사용하지 못하게 된다.
  • H(P, Q)
    • 집합 S상 확률분포 P에 대한 확률분포 Q의 교차 엔트로피
    • 확률분포 P에서 i(A_j)의 평균
      • H(P, Q) = sigma(P(A_j)i(A_j))j = -sigma(P(A_j)(log_2)Q(A_j))j = -sigma(P(x)(log_2)Q(x))x∈X
        • 이 값은 정확한 확률분포 P를 사용했을 때의 비트수보다 크게 된다. 따라서 이 값은 P와 Q가 얼마나 비슷한지를 표현한다.
          • 같으면 H(P, Q) = H(P)
          • 다르면 H(P, Q) > H(P)
        • Q(X)를 가정하고 코드를 부여한다.
          • 평균비트수
            • 3 x 1/2 + 3 x 1/4 + 2 x 1/8 + 1 x 1/8 = 21 / 8 비트
            • 1.5배나 더 많은 비트를 사용해야 한다.
  • 분류 문제에서의 손실함수
    • 분류문제
      • 주어진 대상이 A인지 아닌지 판단
      • 주어진 대상이 A,B,C, ... 중 어느 것인지 판단
    • 기계학습에선 주어진 대상이 각 그룹에 속할 확률을 제공한다.
      • ex) [0.8, 0.2] : A일 확률 0.8, 아닐 확률 0.2
      • 이 값이 정답과 얼마나 다른지 측정이 필요하다.
    • 원하는 답 P = [p_1, p_2, ... , p_n], p_1 + p_2 + ... + p_n = 1
      제시된 답 Q = [q_1, q_2, ... , q_n], q_1 + q_2 + ... + q_n = 1
      
      • P와 Q가 얼마나 다른지에 대한 척도가 필요하다.
    • 제곱합
      • sigma(p_i - q_i)^2
      • 확률이 다를수록 큰 값을 가지지만 학습 속도가 느리다.
    • 교차 엔트로피 H(P, Q)
      • 확률이 다를수록 큰 값을 가지며, 학습 속도가 빠르다.
      • 분류 문제에서 주로 교차 엔트로피를 사용한다.

확률 (probability)

상대 도수에 의한 정의이다.

확률의 고전적 정의

• 표본공간 (sample space)
  • 모든 가능한 실험결과들의 집합
• 사건 - 대문자로 표현
  • 관심있는 실험결과들의 집합
  • 표본 공간의 부분집합
• 어떤 사건이 일어날 확률 - P로 표현
  • 표본 공간의 모든 원소가 일어날 확률이 같은 경우
  • 사건의 원소의 수 / 표본공간의 원소의 수
  • 확률은 0에서 1사이의 값을 가짐
    • 1은 무조건 사건이 일어남
    • 0은 절대 사건이 일어나지 않음

ex) 주사위를 2번 던졌을 때 합이 10일 확률

표본공간 = { ( 1, 1 ), ( 1, 2 ), ( 1, 3 ), ... , ( 6, 6 ) } 총 36가지

합이 10일 사건 A = { ( 4, 6 ), ( 5, 5 ), ( 6, 4 ) } 총 3가지

확률 P(A) = 3/36 = 1/12

확률의 계산

조합 (combination)이란? 어떤 집합에서 순서에 상관없이 뽑은 원소의 집합

n개 중 r개를 뽑는 조합의 수

덧셈 법칙 (Addition Law)

• 사건 A나 사건 B가 일어날 확률
  • P(A∪B)
• 사건 A와 사건 B가 동시에 일어날 확률
  • P(A∩B)
• P(A∪B) = P(A) + P(B) - P(A∩B)

서로 배반 (Mutually Exclusive)

• 두 사건의 교집합이 공집합일 경우 사건 A와 사건 B가 서로 배반한다고 한다.
  • P(A∩B) = 0
  • P(A∪B) = P(A) + P(B)

조건부 확률 (Conditional probability)

• 어떤 사건 A가 일어났을 때, 다른 사건 B가 일어날 확률
• P(B|A) = P(A∩B)/P(A)
• 단, P(A) > 0

ex) 주사위를 하나 던졌는데, 4이상의 수가 나왔다. 이 때 그 수가 짝수일 확률은?

사건 A : 4 이상의 수가 나오는 확률 

사건 B : 짝수가 나오는 사건

P(B|A) = P(A∩B)/P(A) = (1/2) / (1/3) = 2/3

곱셈 법칙 (Multiplication law)

• P(B|A) = P(A∩B)/P(A)
• P(A∩B) = P(B|A)P(A)

ex) 어떤 학교에서 60%의 학생이 남학생이다. 그 학교 남학생의 경우 80%는 축구를 좋아한다. 그 학교에서 학생 1명을 랜덤하게 뽑았을 때 축구를 좋아하는 남학생일 확률은?

P(A∩B) = P(B|A)P(A) = 0.8 * 0.6 = 0.48

서로 독립 (Mutually Independent)

• P(B|A) = P(B)인 경우 사건 A와 B는 서로 독립이라고 한다.
• P(A∩B) = P(B|A)P(A) = P(B)P(A) = P(A)P(B)

여사건

• 사건 A의 여사건
  • 사건 A가 일어나지 않을 사건
  • A^c로 표시
• 어떤 사건과 그 여사건은 서로 배반이다. 즉, 둘 중 하나는 반드시 일어난다.
  • P(A∪A^c) = P(A) + P(A^c) = 1
  • P(A) = 1 - P(A^c)

확률의 분할 법칙

그림출처 : 프로그래머스 스쿨

• 사건 B는 다음과 같이 나누어진다.
  • B = (A∩B)∪(A^c∩B)
  • (A∩B)와 (A^c∩B)는 서로 배반
  • ∴ P(B) = P[(A∩B)∪(A^c∩B)] = P(A∩B)∪P(A^c∩B) = P(B|A)P(A) + P(B|A^c)P(A^c)

ex) 어떤 사파리에서 70%가 사자고, 나머지가 호랑이다. 사자는 60%가 2살 이상이고, 호랑이는 40% 정도가 2살 이상이다. 전체 동물 중 2살 이상인 동물의 비율은?

사건 A : 동물이 사자인 사건

사건 B : 동물이 2살 이상인 사건

P(B) = P(B|A)P(A) + P(B|A^c)P(A^c) = 0.6 x 0.7 + 0.4 x 0.3 = 0.54

베이즈 정리

• 처음의 확률
  • 사전 확률 (prior probability)
• 수정된 확률
  • 사후 확률 (posterior probability)
• P(A|B) = P(A∩B) / P(B) = P(B|A)P(A) / P(B|A)P(A) + P(B|A^c)P(A^c)

ex) 앞 예제에서 동물 한 마리를 랜덤하게 선택했는데, 이 동물이 2살 이었다. 이 동물이 사자일 확률은?

P(A|B) = P(A∩B) / P(B) = P(B|A)P(A) / P(B|A)P(A) + P(B|A^c)P(A^c) = 0.6 x 0.7 / 0.6 x 0.7 + 0.4 x 0.3 = 0.78

그림출처 : 프로그래머스 스쿨

ex) 어떤 사람이 검은색과 흰색의 셔츠를 갖고 있는데, 매일 아침 3/4 정도는 검은색 셔츠를 입고, 1/4 정도는 흰색 셔츠를 입는다. 이 사람이 검은색 셔츠를 입었을 때는 3/4 정도 넥타이를 매고, 흰색 셔츠를 입었을 땐 1/2 정도 넥타이를 맨다 하자. 어느 날 이 사람이 넥타이를 맸다면 이 사람이 검은색 셔츠를 입었을 확률을 구하라.

사건 A : 아침에 검은색 셔츠를 입는 사건 P(A) = 3/4

사건 B : 넥타이를 맨 사건 P(B|A) = 3/4, P(B|A^c) = 1/4

구하는 확률

P(A|B) = (3/4)x(3/4)/(3/4)x(3/4)+(1/2)+(1/4) = 9/11

확률 변수 (random variable)

• 랜덤한 실험 결과에 의존하는 실수. 표본 공간의 부분 집합에 대응하는 실수
• 보통 표본 공간에서 실수로 대응되는 함수로 정의
• 보통 X나 Y 같은 대문자로 표시
  
  

이산확률변수 (discrete random variable)

확률변수가 취할 수 있는 모든 수 값들을 하나씩 셀 수 있는 경우

연속확률변수 (continuous random variable)

셀 수 없는 경우

확률 분포 (Probability Distribution)

확률변수가 가질 수 있는 값에 대해 확률을 대응시켜주는 관계

ex) 어떤 확률 변수 X가 가질 수 있는 값 : 0, 1, 2, 3

각 값이 나올 확률

P(X=0) = 0.5

P(X=1) = 0.2

P(X=2) = 0.2

P(X=3) = 0.1

ex) 주사위 2개를 던지는 실험

확률 변수 X : 주사위 숫자의 합

X가 가질 수 있는 값

2, 3, ..., 12

P( X = 12 ) = 1 / 36

확률 변수 Y : 주사위 숫자의 차

Y가 가질 수 있는 값

0, 1, 2, ..., 5

P( Y = 5 ) = 2 / 36 = 1 / 18

확률 변수 X는 주사위를 던질 때마다 값이 달라질 수 있다.

n번 실험하면, n개의 숫자가 나온다. 이 n개의 숫자의 평균과 분산을 계산할 수 있다.

즉, 확률 변수 X도 평균과 분산을 갖는다. 이 평균과 분산을 모집단의 평균과 분산이라 할 수 있다.

확률분포의 표현

표, 그래프, 함수 등 다양하게 표현 가능하다.

이산확률변수

• 이산확률변수의 확률분포는 보통 함수로 주어진다.
  • 확률변수 X가 x라는 값을 가질 확률
    • P(X = x) = f(x)
    • 확률질량함수
• 이산확률변수의 평균
  • 기대값 (expected value)라고도 한다.
  • E(X) = sigma(xP(X=x)x = sigma(xf(x))x

ex) 만약 100,000번의 실험을 했다면, 

0이 대략 10,000번 나오고,

2이 대략 30,000번 나오고,

5이 대략 60,000번 나왔다고 하면 평균은

0X10000 + 2X30000 + 5X60000 / 100000 = 3.6

• 이산확률변수의 분산
  • 실험을 할 때마다 확률변수의 값은 달라진다. 따라서 그 변동의 정도인 분산을 계산할 수 있다.
  • σ^2 = 1/N(N(sigma(x_i-μ)^2)i=1)
  • (X - μ)^2의 평균
  • σ^2 = E[(X - μ)^2] = (sigma(x - μ)^2)P(X = x) = E(X^2) - {E(X)}^2
  • Var(X)라고도 한다.

ex) 위의 예에서의 분산을 구하면

σ^2 = ((0 - 3.6)^2x10,000 + (2 - 3.6)^2x30,000 + (5 - 3.6)^2x60,000)/100,000 = 3.24

결합확률 분포 (Joint probability distribution)

두 개 이상의 확률 변수가 동시에 취하는 값들에 대해 확률을 대응시켜주는 관계

결합확률분포를 통해 각 확률변수의 확률분포를 도출할 수 있다.

=> 주변확률분포 (marginal probability distribution)

공분산 (Covariance)

두 개의 확률변수의 선형 관계를 나타내는 값

Cov(X, Y) -= E[(X - μ_x)(Y - μ_y)] = E(XY) - μ_xμ_y = E[XY] - E[X]E[Y]

상관계수 (correlation coefficient)

공분산은 각 확률 변수의 절대적인 크기에 영향을 받는다. 따라서 단위에 의한 영향을 없앨 필요가 있다.

ρ = Corr(X, Y) = Cov(X, Y)/σ_xσ_y

이항분포 

베르누이 시행 (Bernoulli trial)

정확하게 2개의 결과만을 갖는 실험. ex) 동전 던지기

보통 성공과 실패로 결과를 구분하며, 성공의 확률을 p라고 한다.

이항확률변수

확률변수 X는 n번의 베르누이 시행에서 성공의 횟수이다. 

이항분포(binomail distribution)

이항확률변수의 확률분포이다.

ex) 어떤 랜덤박스의 뽑기 성공 확률이 0.2이다. 3개를 뽑았을 때, 적어도 하나 이상의 성공이 발생할 확률은?

• 평균
  • E(X) = np
• 분산
  • Var(X) = np(1-p)
• 표준편차
  • SD(X) = root(np(1-p))

정규분포

연속확률 변수의 확률 분포. 확률밀도함수(probability density function)로 표현한다.

P[a ≤ X ≤ b] = b(integral(f(x)dx))a

그래프의 넓이가 확률이 된다.

정규분포의 확률밀도함수

X ~ N (μ, σ^2) => 평균이 μ고, 분산이 σ^2인 정규분포를 따른다는 뜻이다.

표준정규확률변수 (standard normal random variable)

Z = X - μ / σ

표준정규분포 (standard normal distribution)

Z ~ N (0, 1)

표준 정규분포표 => P[Z ≤ z]

ex) X~N(4, 3^2)

P[X ≤ 4]

= P[X - μ / σ ≤ 4 - μ / σ]

= P[Z ≤ 4-4 / 3] = P[Z ≤ 0]

=0.5

ex2)

P[4 ≤ X ≤ 7]

= P[X ≤ 7] + P[X < 4]

= P[Z ≤ 7-4 / 3] - P[Z < 0]

= P[Z ≤ 1 ] - P[Z < 0] = 0.8413 - 0.5 = 0.3413

포아송 분포 (Poisson distribution)

일정한 시간단위 또는 공간 단위에서 발생하는 이벤트의 수의 확률분포

확률분포함수 (확률질량함수)

P[X = x] = f(x) = λ^x(e^-λ / x!), x = 0,1, 2, ...

평균 : λ

분산 : λ

ex) 어느 웹사이트에 시간당 접속자 수는 평균이 3 (λ = 3)인 포아송 분포를 따른다고 할 때, 앞으로 1시간 동안 접속자 수가 2명 이하일 확률은? 

P [X ≤ 2] = P [X = 0] + P [X = 1] + P [X = 2] = 3^0(e^-3 / 0!) + 3^1(e^-3 / 1!) + 3^2(e^-3 / 2!)

= 0.04998 + 0.14936 + 0.22404 = 0.42319

지수분포 (Exponential distribution)

포아송 분포에 의해 어떤 사건이 발생할 때, 어느 한 시점으로부터 이 사건이 발생할 때까지 걸리는 시간에 대한 확률 분포

확률밀도 함수

f(t) = λe^(-λt)

λ : 포아송 분포 평균

평균 : E(T) = 1 / λ

분산 : Var(T) = 1 / λ^2

ex) 어느 웹사이트에 시간당 접속자 수는 λ = 3인 포아송 분포를 따른다 한다. 지금부터 시작하여 첫번째 접속자가 30분 이내 올 확률은?

P[T ≤ 0.5] = 0.5(integral(λe^(-λt))0)dt = 0.5(integral(3e^(-3t))0)dt = 0.5([-e^(-3t)])0 = 1-e^(-1.5) = 1-0.2231 = 0.7769